2015-06-10
932
5. Из урны, содержащей 2 белых и 3 черных шара, случайным образом и без возвращения извлекаются 3 шара. Случайная величина Х – число черных шаров в выборке. Найти:
а) закон распределения дискретной случайной величины Х;
б) числовые характеристики: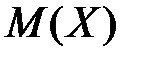 
, 
, 
;
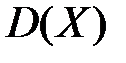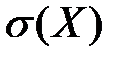в) аналитическую функцию распределения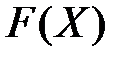 
и построить график этой функции.
6. Непрерывная случайная величина Х задана функцией распределения
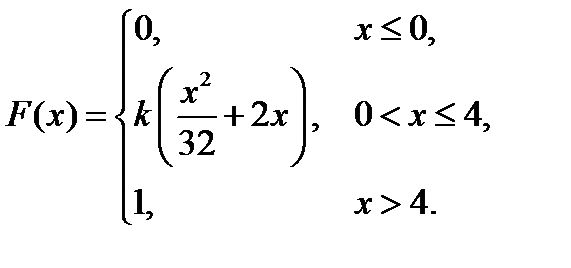
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а =10 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (5, 9); б) отклонения этой величины от математического ожидания не более, чем на d=7.
8. Найти коэффициент корреляции двумерной случайной величины (Х,У), заданной
матрицей:
| у\х | -2 | ||
| -3 | 0.3 | 0.2 | 0.1 |
| 0.2 | 0.1 | 0.1 |
Семестр 4
ВЫСШАЯ МАТЕМАТИКА
