Плотность вероятности

Отметим, что вероятность попадания НСВ в заданную точку равна нулю. Действительно, =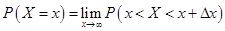

= =0.

Поэтому, можно говорить только о вероятности попадания ДСВ в некоторый интервал. Вероятность попадания случайной величины 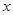в интервал 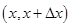обозначим : .

.

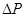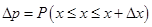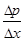
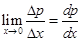
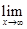Распределение НСВ обычно задается плотностью вероят­ности 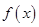, которая определяется как производная функции распределения:

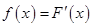
(3.22)

Смысл функции 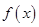выясним из преобразований

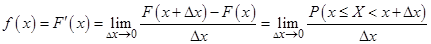
т. е. 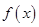–это вероятность попадания случайной величины в бесконечно, малый интервал длиной 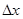, стягивающийся к точке х.

Пример 3.21. Найдем плотность вероятности для случайной величины, определенной функцией распределения (3.20);

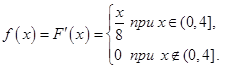
(3.23)

График функции распределения показан на рис. 4.

Свойства плотности вероятности:

1) ;

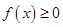2) 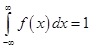– условие нормировки для НСВ;

3) .

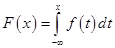Если задана плотность вероятности НСВ X, то вероят­ность ее попадания в интервал 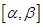находится по формуле

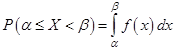
(3.24)