Математическим ожиданием случайной величины X (обозначается 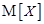 или
или 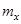 )называется величина
)называется величина
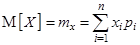
| (3.25) |
Вероятностный смысл математического ожидания ДСВ – это число, около которого группируются средние значения случайной величины с ростом числа испытаний.
Математическое ожидание непрерывной случайной величины вычисляется по формуле
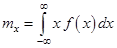 . .
| (3.26) |
Пример 3.21.
Пусть распределение ДСВ задано таблицей:
Таблица 3.1
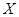
| ||||
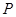
| 0,1 | 0,2 | 0,4 | 0,3 |
Найти математическое ожидание 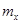 .
.
Решение
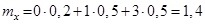 .
.
Пример 3.22.
Пусть распределение НСВ задано плотностью вероятности (3.24):
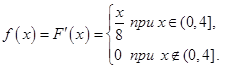
| (3.27) |
Найти математическое ожидание 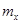 .
.
Решение
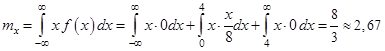
 2015-06-10
2015-06-10 317
317








