Этапы и структура моделирования

Процесс моделирования включает в себя Следующие шаги:

1) построение модели;

2) изучение модели;

3) экстраполяцию — перенос полученных данных на область знаний об исходном объекте.

На первом этапе при осознании невозможности или нецелесообразно­сти прямого изучения объекта создаётся его модель. Целью этого этапа является создание условий для полноценного замещения оригинала объектом-посредником, воспроизводящим его необходимые параметры.

На втором этапе производится изучение самой модели, настолько детальное, насколько это требуется для решения конкретной познава­тельной задачи. Здесь исследователь может осуществлять наблюдения за поведением модели, проводить над ней эксперименты (модельный эк­сперимент), осуществлять измерение или описание её характеристик. Это зависит от специфики самой модели и от исходной познаватель­ной задачи. Целью второго этапа является получение требуемой ин­формации о модели.

Необходимо отметить, что, хотя модель мы создаём (или выбираем) сами, подчиняя её ряду условий, она, тем не менее, обладает определённой самостоятельностью. В ней присутствует некий элемент неизвестности, поэтому модель надо действительно изучать, и она в должной мере заранее неизвестна. Метод моделирования потому и относится к эмпирическим методам, что предполагает интерактивный режим работы с изучаемым явлением (в данном случае с моделью, а также в той или иной мере — и с оригиналом).

Третий этап (экстраполяционный) представляет собой возвращение к исходному объекту, т.е. интерпретацию полученных знаний о модели, оценку их приемлемости и, соответственно, непосредственное примене­ние их к оригиналу, позволяющее в случае успеха решить исходную по­знавательную задачу (см. рис. 2).

Эти шаги реализуют своеобразный цикл моделирования, в ходе кото­рого модель и оригинал соотносятся друг с другом.

Роль модели достаточно интересна, т.к. она является одновременно и объектом, и средством изучения. Модель по своей познавательной функции принципиально транзитивна, т.е. сопряжена с другим объектом: изучая модель, мы постоянно нацелены на её прототип.

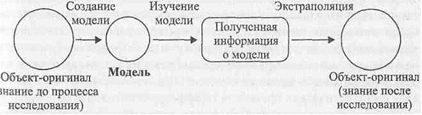Рис. 2. Этапы моделирования

Исходя из этапов моделирования легко увидеть, что структура метода моделирования содержит больше компонентов, чем наблюдение или экспе­римент. В моделирование включены следующие составляющие:

1) субъект, осуществляющий моделирование;

2) моделируемый объект — оригинал;

3) объект-посредника — модель;

4) контекст моделирования, к которому относятся условия времени и ме­ста, концептуальные и материально-технические средства.

При построении модели исходного объекта часто происходит его упро­щение и вводятся некоторые допущения (как правило, идеализирующие си­туацию). Допущения и базирующиеся на них понятия могут быть и весьма абстрактными, как, например, при математическом моделировании (скажем, понятие абстрактного инфекционного процесса при моделировании иммун­ных процессов). Исходные допущения должны быть осознанными и обосно­ванными, т.к. неверные допущения приведут к серьёзным искажениям при экстраполяции. Это означает, что для всякой модели следует чётко формули­ровать объем задач, которые будут решаться с её помощью:

Надо помнить и о том, что исходный объект может быть воспроизве­дён с помощью разных моделей; в общем случае нельзя сказать, что ка­кая-то из них является истинной, настоящей, правильной. Достоинства той или иной модели в полной мере зависят от конкретной цели исследо­вания, от концептуального угла зрения учёного.

Классификация моделей

Назовём некоторые основания классификации моделей:

1) по субстрату — материальные (вещественные) и идеальные (концеп­туальные, мысленные);

2) по моделируемым аспектам — структурные, функциональные и др.; I

3) по виду сходства между оригиналом и моделью — физические, анало­говые, квазианалоговые и др.

Деление по субстрату модели означает различие моделей относи­тельно того, с помощью чего моделируется исходный объект. Здесь для] обозначения конкретного способа моделирования часто используют на­звание материала (пластмассовая модель самолёта и т.п.), характеристи­ку происхождения данной модели (лабораторное животное как естест­венная модель для изучения физиологических процессов у человека) или общего типа моделирующей среды (маятник как механическая мо­дель колебательных процессов, термостат как термодинамическая мо­дель физиологических процессов терморегуляции и т.п.).

Идеальные (концептуальные) модели тоже могут быть представлены разными субстратами: они могут быть графическими, логическими, мате-

матические (среди них есть алгебраические, геометрические, топологиче­ские и т.п.) и многими другими. Но следует помнить о том, что о моделиро­вании в собственном смысле мы говорим лишь тогда, когда наличествуют его необходимые признаки (в т. ч. эвристическая ценность), а не просто имеется некоторая форма представления знаний, называемая моделью. На­пример, географическая карта может не только выступать способом хране­ния знаний, но и применяться в моделирующем исследовании: в том слу­чае, когда мы анализируем пути на карте и выбираем наилучший, мы актуально используем и изучаем графическую модель для решения конкрет­ной задачи. Моделирование с применением концептуальной модели — это особое эмпирико-теоретическое исследование; здесь могут использоваться мысленное экспериментирование, вычислительные эксперименты и т.п.

Деление по моделируемым аспектам означает различие моделей отно­сительно того, что именно моделируется в данной ситуации. Ведь модель всегда отражает лишь какие-то отдельные, имеющие интерес для иссле­дователя стороны оригинала. Здесь тоже возможно разнообразие видов моделирования. Модель может воспроизводить структуру объекта (струк­турная), какие-то его функции (функциональная), параметры, особенности формы, каналы управления (кибернетическая), информационные потоки, состояния, связи (например, причинно-следственные), этапы истории и многое другое.

Классификация по виду сходства используется для уточнения того,
в каком именно отношении сходства находятся между собой оригинал
и модель. Часто это имеет важное значение: знание точных соотношений
между оригиналом и моделью оказывается необходимым в физике, в тех­нических науках. Для обозначения этих видов сходства в специальных
дисциплинах применяют особые термины. В случае тождества физической природы изучаемых явлений говорят о физическом подобии (напри­мер, электрические свойства исходного объекта изучают с помощью электрических свойств модели; то же касается свойств механических, жидкостных, оптических и т. п.). Аналоговое моделирование (или использование модели-аналога) — это способ воспроизведения, при котором физическая природа оригинала и модели различна, но математически они описываются одними и теми же уравнениями (например, колебательные процессы в цепи с током и в механической системе); различают также квазианалоговое моделирование (когда математические описания модели и её прототипа отличаются, но эквивалентны относительно получаемых результатов) и другие его виды. Проблему сходства модели и оригинала мы подробнее рассмотрим чуть ниже. <

В названиях моделей, используемых на практике для их характеризации, часто пересекаются сразу несколько оснований классификации. Так,

термин «теоретико-игровая модель», сообщая нам, что данная модель ос­нована на методах математической теории игр, указывает сразу и на то, что эта модель относится к концептуальным, и на то, что моделирующей средой выступает контекст теории игр, и на аспекты, которые ею модели­руются (в данном случае это будут какие-то стратегии поведения в неко­торой конфликтной ситуации).

Рассмотренные способы классификации показывают, что существует обширное множество разновидностей моделей и способов моделирова­ния. Тем не менее, метод моделирования в своих базисных чертах являет­ся единым, несмотря на разнообразие частных модификаций. Не должно вызывать затруднения и то, что в конкретных областях научного позна­ния в понятие «модель» иногда вкладывается специфический смысл. Скажем, в математической логике термин «модель» имеет специальное значение: там моделью формальной теории называется некоторый ма­тематический объект, для которого высказывания теории оказываются истинными. Но и такой смысл понятия «модель» совместим с общемето­дологическим, ведь модель в математическом смысле тоже является объектом-посредником относительно формальной теории, средством увидеть эту теорию в действии, т.к. будучи непроинтерпретированной, вне своих моделей она является лишь чистой формой, которой мы пока не придали никакого смысла. Таким образом, общий смысл термина «мо­дель» сохраняется и при специфическом использовании его в математи­ческой логике.

Проблема сходства оригинала и модели

Для решения многих задач, в которых используется моделирование, требуется уточнить интуитивное понимание того, что модель похожа на оригинал. Знание точных взаимоотношений модели и оригинала позволя­ет на всех этапах моделирования действовать более адекватно: от этапа построения модели с заданными характеристиками до экстраполяции, осуществляемой по строгим правилам.

В физико-технических науках для обозначения обобщённого отно­шения сходства модели и оригинала используется термин «подобие». В физике существует особая дисциплина — теория подобия; она обес­печивает концептуальную поддержку моделирования. В теории подо­бия разрабатываются методы, с помощью которых можно репрезенти­ровать данные как зависимости между безразмерными величинами, т.е. в некотором нейтральном виде; тогда явления, которые описываются одинаковыми значениями безразмерных величин, являются подобны­ми друг другу. Пользуясь этой теорией, исследователь может, изучая явление на какой-либо модели, переносить полученные результаты на

совершенно иные явления, но характеризующиеся теми же значения­ми безразмерных величин. При точном моделировании оперируют и такими понятиями, как масштабы (отношения, устанавливающие условия перехода от модели к оригиналу), критерии подобия (крите­рии адекватного сходства модели и оригинала); выделяют также раз­личные виды подобия — абсолютное, полное, неполное, приближен­ное. У истоков теории подобия стояли Г. Галилей и И. Ньютон. Так, Г. Галилей показал, что сходство механических систем базируется не просто на интуитивно понимаемом сходстве их по внешнему виду и т.п., а на определённых физических соотношениях. И. Ньютон, продолжая этот подход, сформулировал две теоремы подобия для механических систем.

Для обозначения ещё более широкого отношения сходства между объек­тами, системами, процессами предлагают также использовать термин «изо­морфизм» — понятие, пришедшее из абстрактной алгебры. Две сравнивае­мые системы называются изоморфными, если каждому элементу одной системы взаимно однозначно соответствует элемент второй системы, а каж­дому отношению между элементами первой системы соответствует отноше­ние второй системы, имеющее такие же структурные свойства. В контексте моделирования две системы называют изоморфными, если между ними мо­жет быть установлено взаимное соответствие по некоторым изучаемым свойствам. Например, у информационных процессов могут быть выделе­ны устойчивые общие черты, позволяющие им протекать сходным обра­зом в биологическом объекте, компьютере, социальной системе, тогда все эти объекты рассматриваются как изоморфные относительно протекания их информационных процессов.

Взаимное соответствие определённых аспектов двух систем может быть обнаружено и реализовано различными способами. Наиболее яр­ким случаем такого соответствия является изоморфизм структур. При моделировании этого сходства исследователь пытается воспроизвести структурные особенности одной системы на ином субстрате. В бионике для нужд технических наук создаются искусственные аналоги объектов или процессов, обнаруженных в живой природе: например, ультразвуко­вая эхолокация имитирует соответствующие органы животных. Струк­турное моделирование также широко используется в медицинских науках при протезировании органов. Другим вариантом соответствия является существенное сходство функции (поведения). Один и тот же эффект мо­жет быть реализован в системах с совершенно разными структурами: летательный аппарат может быть выполнен не обязательно на основе крыла, но и на основе пропеллера, баллона с лёгким газом, реактивного двигателя.