Агафонова Н.Ю.
Сборник задач по теории вероятностей и математической статистике:
Учеб. пособие для студентов дневного отделения факультета нано- и биомедицинских технологий
Пособие содержит краткие теоретические сведения и задачи по основным разделам теории вероятностей и математической статистике.
Для студентов дневного отделения факультета нано- и биомедицинских технологий. Оно может быть использовано также студентами дневных отделений факультетов, на которых курс «Теория вероятностей и математическая статистика» преподается в объеме семестрового курса.
УДК 519.2(0.75.4)
© Агафонова Н.Ю., 2010
© Саратовский государственный
университет, 2010
ОГЛАВЛЕНИЕ
| Введение | ||
| Глава 1. | Классическое и геометрическое определения вероятности | |
| Глава 2. | Условная вероятность. Теоремы умножения и сложения вероятностей | |
| Глава 3. | Формула полной вероятности и формула Байеса | |
| Глава 4. | Схема независимых испытаний Бернулли. Предельные теоремы в схеме Бернулли | |
| Глава 5. | Дискретные случайные величины и их характеристики | |
| Глава 6. | Непрерывные случайные величины и их характеристики | |
| Глава 7. | Элементы математической статистики | |
| Список литературы | ||
| Приложения |
Введение
Настоящее учебное пособие содержит задачи и краткие теоретические сведения по основным разделам теории вероятностей и математической статистики в объеме, необходимом для их решения. Выбор разделов был обусловлен спецификой преподавания данного предмета на факультете нано-и биомедицинских технологий, а именно тем, что учебным планом предусмотрено только 17 часов практических занятий. По этой причине возникла необходимость в компактном задачнике, содержащем все темы учебного плана. В связи с этими обстоятельствами пособие имеет структуру, соответствующую семинарам: выделены разделы для работы в аудитории и самостоятельной работы.
Как правило, задачи из раздела для самостоятельной работы идентичны задачам из раздела для работы на семинаре и направлены на закрепление полученных знаний. Однако каждый раздел содержит и более сложные задачи. Глава, посвященная математической статистике, построена по другому принципу и содержит варианты для самостоятельной работы в силу того, что вообще задачи по статистике требуют много вычислений и проводить их в аудитории нецелесообразно.
Сборник задач составлен в соответствии с изложением материала в [7] и [8].
Глава 1. Классическое и геометрическое определения вероятности
Будем говорить, что произведен стохастический эксперимент, если результат этого эксперимента нельзя указать заранее. При этом известно множество возможных результатов эксперимента и это множество не изменяется при повторных экспериментах. Кроме того, стохастический эксперимент допускает возможность многократного повторения.
Определение. Элементарным исходом эксперимента 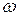 называется результат, которым завершился стохастический эксперимент.
называется результат, которым завершился стохастический эксперимент.
Множество элементарных исходов эксперимента обозначается 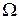 . Записывают
. Записывают 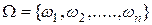 .
.
Определение. Случайным событием 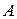 называется любое подмножество множества элементарных исходов экперимента
называется любое подмножество множества элементарных исходов экперимента 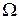 , т.е.
, т.е. 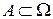 ,
, 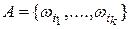 , где
, где 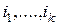 – некоторая перестановка индексов элементов множества
– некоторая перестановка индексов элементов множества 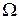 .
.
 2015-06-10
2015-06-10 327
327







