2015-06-10
341
Пусть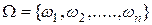 
– конечное множество равновозможных исходов, а 
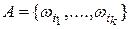–некоторое событие. Тогда вероятность события 
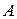вычисляется по формуле:
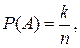(1.1)
где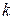 
– количество иcходов, благоприятствующих событию 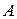, а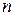 
–общее количество исходов эксперимента.
Задача.
В урне находится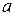 
белых и 
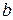черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.
Решение.
Стохастический эксперимент состоит в извлечении одного шара из урны, следовательно, элементарный исход эксперимента можно определить как «извлечен один шар».
Для указания множества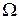 
необходимо перечислить все мыслимые в данном эксперименте исходы. Для рассматриваемого эксперимента можно записать: 
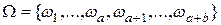. Тогда событие 
.
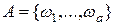Таким образом,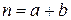 
, 
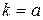, и вероятность события 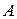равна
.
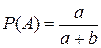Сведения из комбинаторики.
При нахождении вероятностей в схеме классического определения используются элементы комбинаторики. Приведем некоторые необходимые определения.
Пусть имеется конечное множество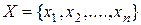 
некоторых элементов.
Определение. Сочетанием из 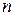элементов множества 
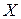по 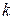называется любое подмножество { 
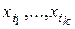} содержащее 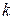элементов, то есть сочетания представляют собой подмножества, различающиеся только составом элементов.
Число всех сочетаний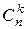 
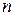(из элементов по 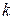) вычисляется по формуле:
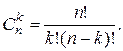(1.2)
Пример. Пусть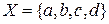 
– множество букв латинского алфавита. Составим сочетания из 4 по 3. Получаем: 
.
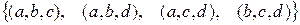Определение. Размещением из 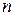элементов множества 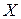по 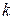элементам (из 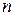элементов по 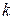) называется любой упорядоченный набор (
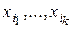) элементов множества Х.
Таким образом, размещения представляют собой такие подмножества, в которых различают не только состав, но и порядок следования элементов.
Число всех размещений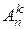 
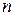(из элементов по 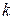) определяется формулой:
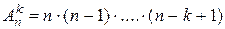. (1.3)
Пример. Пусть по-прежнему 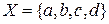– множество букв латинского алфавита. Составим теперь размещения из 4 по 3. Получаем: 
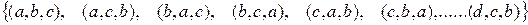. Всего 24 размещения.
Определение. Перестановкой из 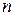элементов по 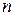называется размещение 
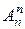(другими словами, 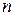элементов по 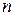местам).
Число всех перестановок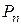 
вычисляется по формуле:
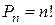(1.4)
