Задана непрерывная случайная величина Х своей функцией распределения F(x). Требуется: 1) найти плотность распределения вероятностей f(x); 2) схематично построить графики F(x) и f(x); 3) найти математическое ожидание и дисперсию X.
1. 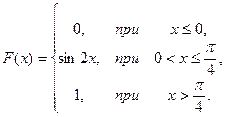 2.
2. 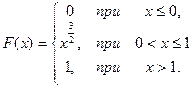
3. 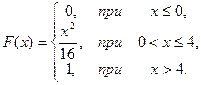 4.
4. 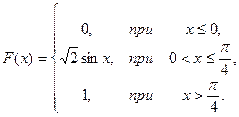
5. 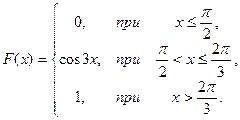 6.
6. 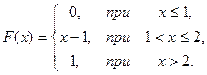
7. 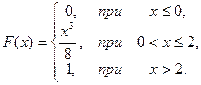 8.
8. 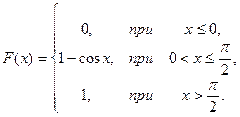
9. 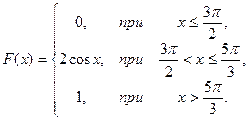 10.
10. 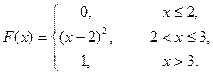
11. 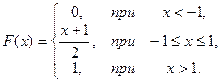 12.
12. 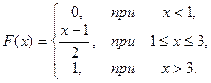

13. 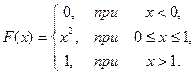 14.
14. 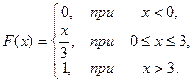

15. 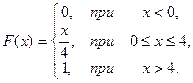 16.
16. 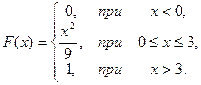
17. 
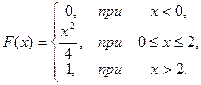 18.
18. 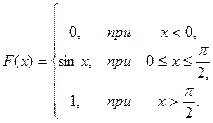
19. 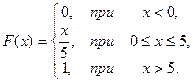 20.
20. 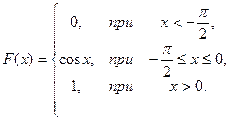
21. 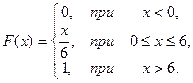 22.
22. 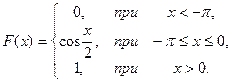
23. 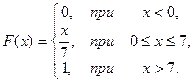 24.
24. 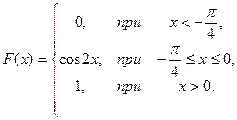
25. 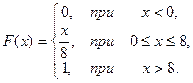
Задача №6
Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения: х1 с вероятностью р1 и х2 с вероятностью р2, причем х1 < х2. Математическое ожидание М(Х) и дисперсия D(X) известны.
1. р1= 0,9, М(Х)= 4,1, D(X)= 0,09.
2. р1= 0,7, М(Х)= 3,3, D(X)= 0,21.
3. р1= 0,1, М(Х)= 5,8, D(X)= 0,36.
4. р1= 0,2, М(Х)= 2,6, D(X)= 0,64.
5. р1= 0,1, М(Х)= 1,9, D(X)= 0,09.
6. р1= 0,3, М(Х)= 3,1, D(X)= 1,89.
7. р1= 0,5, М(Х)= 3, D(X)= 1.
8. р1= 0,4, М(Х)= 2,6, D(X)= 0,24.
9. р1= 0,6, М(Х)= 3,2, D(X)= 2,16.
10. р1= 0,8, М(Х)= 3,4, D(X)= 0,64.
11. р1= 0,1, М(Х)= 2,5, D(X)= 2,25.
12. р1= 0,2, М(Х)= 3,4, D(X)= 1,44.
13. р1= 0,3, М(Х)= 2,4, D(X)= 0,84.
14. р1= 0,4, М(Х)= 2,6, D(X)= 0,24.
15. р1= 0,5, М(Х)= 3, D(X)= 1.
16. р1= 0,6, М(Х)= 2,8, D(X)= 0,96.
17. р1= 0,7, М(Х)= 1,6, D(X)= 0,84.
18. р1= 0,2, М(Х)= 2,2, D(X)= 2,56.
19. р1= 0,2, М(Х)= 1,2, D(X)= 2,56.
20. р1= 0,7, М(Х)= -1,5, D(X)= 5,25.
21. р1= 0,4, М(Х)= 1,8, D(X)= 2,16.
22. р1= 0,6, М(Х)= 1,8, D(X)= 0,96.
23. р1= 0,8, М(Х)=-2,2, D(X)= 2,56.
|
|
|
24. р1= 0,9, М(Х)= -1,5, D(X)= 2,25.
25. р1= 0,7, М(Х)=-1,2, D(X)= 7,56.
 2015-06-10
2015-06-10 705
705








