2015-06-10
630
Пусть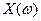 
-- дискретная случайная величина на вероятностном пространстве, принимающая значения 
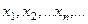. Тогда для каждого 
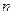определена вероятность
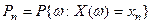где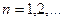 
т.е. СВ принимает заданное значение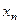 
с вероятностью 
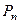. Для того, чтобы найти 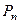, нужно в 
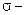алгебре 
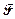выбрать все исходы эксперимента, в результате которых СВ приняла значение 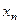и объединить их в событие. Вероятность этого события и есть вероятность того, что случайная величина приняла значение .
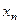Пример. Стохастический эксперимент-бросание двух игральных костей. Случайная величина – сумма выпавших очков на двух костях. Найти вероятность того, что выпадет 6 очков.
Пространство элементарных событий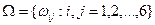 
. Вероятность одного исхода (элементарного события) равна 
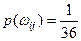. Объединим в событие исходы, при которых выпадает суммарное число очков, равное 6:
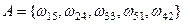. Тогда 
.
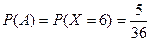Для дискретной случайной величины закон распределения полностью определяется указанием ее значений 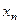(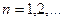) и вероятностей 
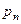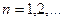(), с которыми случайная величина принимает эти значения.
Ряд распределения СВ – таблица, в которой для каждого значения случайной величины указана вероятность его появления. В случае конечного пространства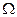 
ряд распределения имеет вид
| Значения случайной
величины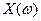
|
|
| … |
|
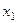
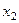
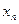
Вероятности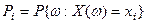 
| 
|  
| … |
|
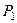
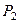
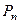
где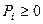 
. и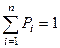 
.
В случае счетного пространства 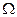ряд распределения может быть представлен таблицей
| Значения случайной
величины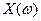
|
|
| … |
| … |
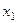
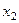
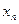
| Вероятности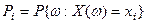
|
|
| … |
| … |
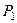
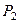
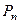
где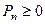 
. и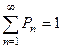 
.
Ряд из вероятностей должен сходиться и иметь сумму, равную единице. В силу необходимого признака сходимости числового ряда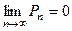 
. Поэтому ряд распределения можно оборвать на некотором значении n.
Графическое изображение ряда распределения называется многоугольником распределения.
Пример. Игрок подбрасывает монету 2 раза. Если выпадает герб, то он получает 1 рубль, если выпадает решетка, то ничего не получает. Случайная величина 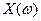– выигрыш игрока. Построить ряд распределения, многоугольник распределения, функцию распределения и ее график.
Пространство элементарных событий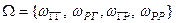 
. Определим события, в результате наступления которых выигрыш игрока равен нулю, единице и двум.
, 
, 
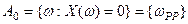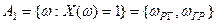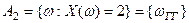. Вероятности этих событий равны соответственно 
, 
, 
.
|
| |||
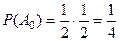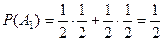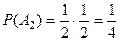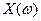
| P |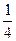 
| 
|
|
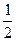
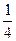
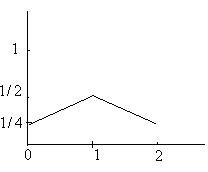
Здесь приведен ряд распределения и многоугольник распределения.
Функция распределения дискретной случайной величины разрывна. Ее график – ступенчатая линия, имеющая разрывы при тех значениях случайной величины, вероятность которых отлична от нуля. Величина скачка в точке разрыва равна вероятности соответствующего значения случайной величины. Для построения графика функции распределения дискретной случайной величины нужно построить таблицу накопленных вероятностей для данной случайной величины и по этой таблице построить соответствующую ступенчатую линию. В данном случае функция распределения случайной величины имеет вид
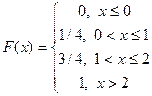
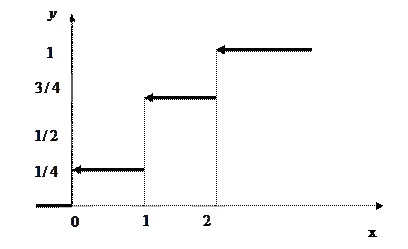
На рис. представлен график функции распределения
. Примеры дискретных случайных величин.
