Пусть производятся независимые испытания и при каждом испытании может быть 2 исхода: успех с вероятностью 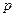 или неудача с вероятностью
или неудача с вероятностью 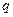 , при этом (
, при этом (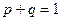 ).
).
Примеры
1) Стрельба по цели. При каждом выстреле 2 исхода: попадание или промах.
2) Проверка наугад выбранного изделия, которое может оказаться качественным или бракованным.
3) Подбрасывание симметричной монеты.Может выпасть герб или решетка.
Построим вероятностную модель эксперимента в случае 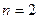 .
.
Пространство элементарных событий 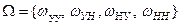 .
.
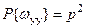 ,
, 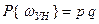 ,
, 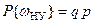 ,
, 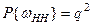 . Поскольку испытания независимы, то вероятности элементарных исходов определяются как произведение вероятностей.
. Поскольку испытания независимы, то вероятности элементарных исходов определяются как произведение вероятностей.
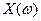 | |||
| P | 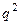 | 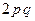 | 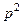 |
В качестве случайной величины 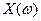 рассмотрим число успехов в серии из 2 испытаний. Построим ряд распределения случайной величины
рассмотрим число успехов в серии из 2 испытаний. Построим ряд распределения случайной величины
При этом 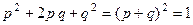 , так как
, так как 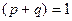 .
.
Пусть теперь опыт повторяется 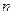 раз. При каждом опыте событие А (успех) происходит с вероятностью
раз. При каждом опыте событие А (успех) происходит с вероятностью 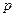 и не происходит с вероятностью
и не происходит с вероятностью 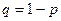 , причем эти вероятности от опыта к опыту не меняются. Случайная величина
, причем эти вероятности от опыта к опыту не меняются. Случайная величина 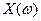 – число успехов в серии из
– число успехов в серии из 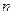 испытаний, Найдем вероятность того, что
испытаний, Найдем вероятность того, что 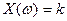 , т.е. что событие А (успех) наступит
, т.е. что событие А (успех) наступит 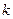 раз (а, следовательно, неуспех наступит
раз (а, следовательно, неуспех наступит 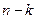 раз).Найдем вначале, что событие А (успех) произойдет при первых
раз).Найдем вначале, что событие А (успех) произойдет при первых 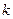 опытах и не произойдет при последних
опытах и не произойдет при последних 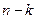 опытах. Применяя теорему умножения вероятностей, получим
опытах. Применяя теорему умножения вероятностей, получим 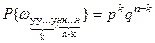 . Но событие А может произойти
. Но событие А может произойти 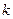 раз и в другой последовательности. Общее число всех возможных последовательностей равно
раз и в другой последовательности. Общее число всех возможных последовательностей равно 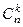 . Вероятность появления события А для каждой такой последовательности равна
. Вероятность появления события А для каждой такой последовательности равна 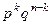 . Вероятность появления какой либо одной из этих последовательностей найдем с помощью теоремы сложения вероятностей
. Вероятность появления какой либо одной из этих последовательностей найдем с помощью теоремы сложения вероятностей
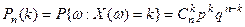 , где
, где 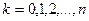 .
.
Полученная формула является формулой для 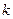 –го члена бинома Ньютона
–го члена бинома Ньютона 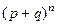 . Поэтому такое распределение вероятностей называется биномиальным. Впервые это распределение подробно изучил Бернулли. Поэтому стохастический эксперимент, приводящий к биномиальному распределению, называется схемой Бернулли.
. Поэтому такое распределение вероятностей называется биномиальным. Впервые это распределение подробно изучил Бернулли. Поэтому стохастический эксперимент, приводящий к биномиальному распределению, называется схемой Бернулли.
Функция распределения биномиального закона имеет вид
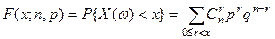 ,
,
где 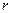 неотрицательное целое число.
неотрицательное целое число.
Пример. Прибор состоит из четырех элементов. Вероятность отказа каждого из них равна 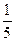 . Найти вероятность отказа 0,1,2,3,4 элементов во время работы прибора.
. Найти вероятность отказа 0,1,2,3,4 элементов во время работы прибора.
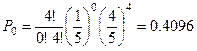
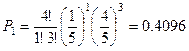
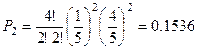
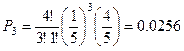
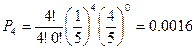
Сумма всех вероятностей равна 1, так как эта сумма есть вероятность достоверного события.
 2015-06-10
2015-06-10 928
928








