1) 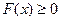 , так как
, так как 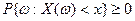 .
.
2) 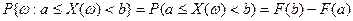
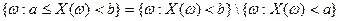 , так как
, так как 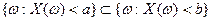 . Отсюда
. Отсюда 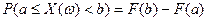 на основании свойства вероятностей:
на основании свойства вероятностей: 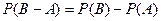 , если
, если 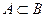 .
.
3) Если 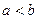 , то
, то 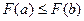 , т.е. функция
, т.е. функция 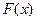 – неубывающая функция.
– неубывающая функция.
Действительно, если 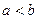 , то
, то 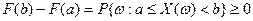 .т.е.
.т.е. 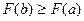 .
.
4) 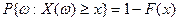 .
.
Это свойство следует из соотношения
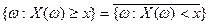
5) 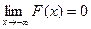 ,
, 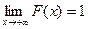 .
.
Это следует из того, что 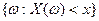 при
при 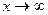 стремится к достоверному событию, а при
стремится к достоверному событию, а при 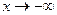 стремится к невозможному событию.
стремится к невозможному событию.
Следовательно, 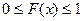 .
.
6) Функция 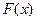 непрерывна слева:
непрерывна слева: 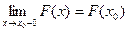 .
.
7) 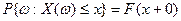
8) 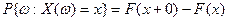 .
.
Действительно, учитывая, что 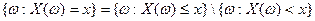 и
и 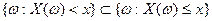 , получим
, получим 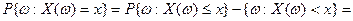
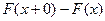 .
.
Отсюда следует, что если функция 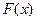 непрерывна в точке
непрерывна в точке 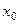 , то
, то 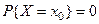 , так как
, так как 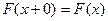 .
.
Теорема. Пусть 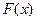 обладает следующими свойствами:
обладает следующими свойствами:
1) 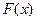 – неубывающая функция на всей числовой оси
– неубывающая функция на всей числовой оси 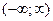 ;
;
2) 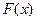 – непрерывна слева в каждой точке оси;
– непрерывна слева в каждой точке оси;
3) 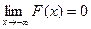 ,
, 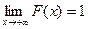 .
.
Тогда существует вероятностное пространство 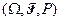 и случайная величина
и случайная величина 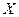 такая, что ее функция распределения равна
такая, что ее функция распределения равна 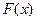 .
.
 2015-06-10
2015-06-10 330
330








