Пусть в урне 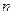 шаров, среди которых
шаров, среди которых 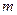 белых и
белых и 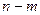 черных шаров. Случайная величина
черных шаров. Случайная величина 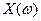 – число белых шаров среди
– число белых шаров среди 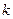 шаров, взятых наугад. Найдем распределение случайной величины
шаров, взятых наугад. Найдем распределение случайной величины 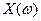 . Число всевозможных партий, содержащих
. Число всевозможных партий, содержащих 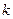 шаров, выбранных из
шаров, выбранных из 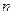 шаров, равно
шаров, равно 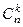 . Среди них имеется
. Среди них имеется 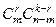 партий, содержащих ровно
партий, содержащих ровно 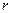 белых шаров. Здесь
белых шаров. Здесь 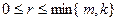 . Вероятность того, что в партии из
. Вероятность того, что в партии из 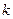 шаров, выбранных из
шаров, выбранных из 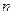 шаров, содержится ровно
шаров, содержится ровно 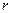 белых шаров равна
белых шаров равна
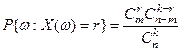 .
.
Этот набор вероятностей называется гипергеометрическим распределением. Функция распределения для гипергеометрического распределения имеет вид
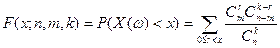 .
.
 2015-06-10
2015-06-10 306
306








