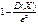Неравенство Чебышева. Закон больших чисел и его следствия

Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа ε будет не меньше, чем

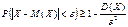т.е.

Неравенство справедливо для дискретных и непрерывных случайных величин.

Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа

Неравенство Чебышева дает оценку вероятности события

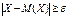для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

Данная тема важна для понимания математической статистики. Она включает ряд теорем, устанавливающих при определенных условиях устойчивость частности и средней арифметической (т. Бернулли, Пуассона, Чебышева, Маркова и др.) или устойчивость закона распределения (т. Ляпунова).

Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных чисел почти утрачивает случайный характер и становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие многих случайных величин приводит к результату, который почти не зависит от случая, тк позволяет предвидеть ход явления. Эти условия и указываются в теоремах, носящих об

общее название закона больших чисел. К ним относятся т. Чебышева - наиболее общий закон, Бернулли- простейший.

Теорема (Теорема Бернулли). Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.

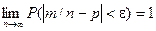
Здесь т – число появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. 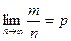(сходимость поточечная). В теореме имеется в виду только сходимость по вероятности, т.е. приближения относительной частоты к вероятности появления события А в каждом испытании.

В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.

Теорема (Теорема Пуассона). Если производится п независимых опытов и вероятность появления события А в каждом опыте различна и равна рi, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей рi.

Теорема даёт возможность определить примерно относительную частоту появления события А.