2015-06-04
1903
В гидравлике уравнение Бернулли чаще всего используется в форме (3.18)
.
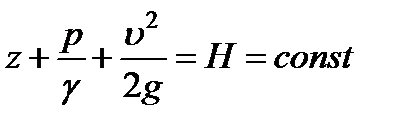Все члены этого уравнения имеют линейную размерность - [м, см]. Подобно тому, как первый член этого уравнения представляет собой некоторую высоту можно и остальные слагаемые представить как высоты. Не следует думать, что речь идёт о каких-то воображаемых высотах. Все эти высоты можно воспроизвести реально. Выделим элементарную струйку, возвышающуюся над горизонтальной плоскостью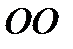 
(рис. 3.10).
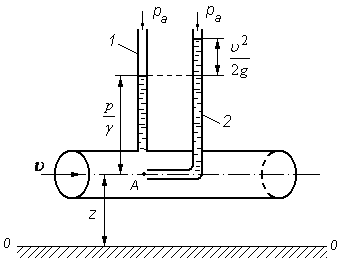
Рис. 3.10. Геометрическая интерпретация уравнения Бернулли
(схема трубки полного давления - Пито)
Каждая из этих высот получила определённое название:
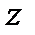- геометрическая или нивелирная высота, т.е. высота центра тяжести поперечного сечения струйки, измеренная относительно некоторой произвольной плоскости сравнения 
;
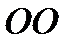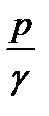- пьезометрическая высота, т.е. высота столба жидкости в трубке пьезометра 1;
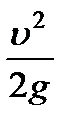- высота скоростного напора, т.е. дополнительная высота, на которую жидкость поднялась бы в пьезометре при полном торможении потока в данной точке А;
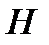- высота полного гидродинамического напора, т.е. сумма указанных трёх высот.
Высота столба жидкости в пьезометре, измеренная относительно точки А, равна пьезометрической высоте в этой точке потока.
Во второй же трубке жидкость поднимется на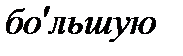 
высоту, поскольку скорость в точке А упала до нуля и удельная кинетическая энергия полностью перешла в энергию давления.
Разность высот в этих двух трубках, таким образом, равна удельной кинетической энергии, или то же самое, высоте скоростного напора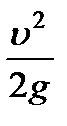 
.
Полный гидродинамический напор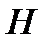 
равен сумме трёх указанных высот.
Закон, выражаемый уравнением Бернулли, может быть наглядно представлен для элементарной струйки в виде диаграммы (рис. 3.11).
Отнесём струйку к системе координат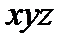 
и напишем уравнение Бернулли для трёх произвольных сечений струйки
.
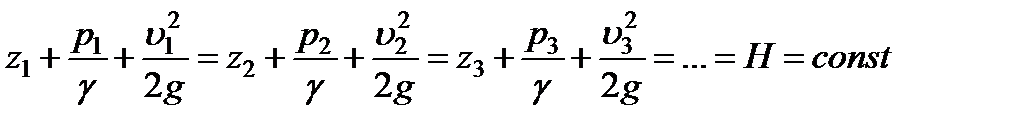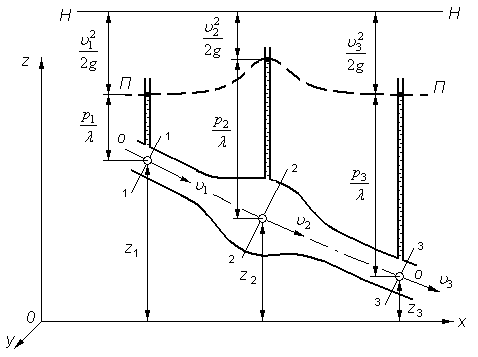
Рис. 3.11. Линии полных напоров Н-Н и пьезометрических
высот П-П вдоль струйки идеальной жидкости
Выбрав произвольно горизонтальную плоскость сравнения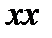 
отложим от неё геометрическую высоту 
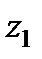поперечного сечения 1-1 струйки. Затем надстроим в том же масштабе последовательно пьезометрическую высоту 
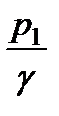и высоту скоростного напора 
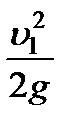. Сумма этих высот равна высоте 
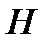полного гидродинамического напора, которая по всей длине струйки идеальной жидкости остаётся одинаковой. На высоте 
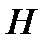расположена горизонтальная линия 
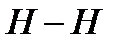, которую принято называть линией полного гидродинамического напора или сокращённо напорной линией.
Теперь в любом другом произвольном сечении струйки (например, в сечении 2-2) можно не зная даже величины давления в этом сечении, построить все три высоты, входящие в уравнение Бернулли. Удобнее всего построение начать с высоты скоростного напора, величина которой может быть легко найдена из геометрии струйки с помощью уравнения расхода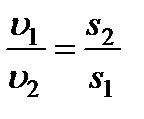 
, 
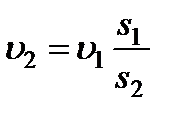. Полученную таким образом высоту 
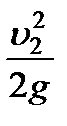отложим вниз от плоскости полного напора. Дополнительный вертикальный отрезок до центра тяжести сечения струйки и будет представлять искомую пьезометрическую высоту 
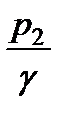, а вертикальный отрезок до центра тяжести сечения до плоскости сравнения 
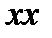- геометрическую высоту 
.
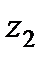Соединяя плавными кривыми вершины всех трёх высот, получаем характерные элементы «диаграммы Бернулли»:
- линию геометрических высот (осевую линию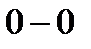 
струйки);
- пьезометрическую линию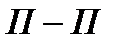 
(геометрическое место вершин пьезометрических высот);
- напорную линию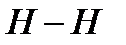 
(геометрическое место вершин высот полного гидродинамического напора).
Итак, рисунок 3.11 даёт геометрическое истолкование уравнения Бернулли:
1) При установившемся движении идеальной жидкости сумма трёх высот есть величина постоянная, и называется полным напором;
2) Если сечение расширяется и, следовательно, скорость уменьшается, то уменьшается скоростной напор, но возрастает сумма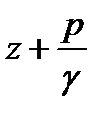 
.
Закономерности, найденные для струйки, справедливы и для одномерных потоков конечного сечения.
