Лунный календарь

Лунный счет времени самый древний. Зачаточные формы лунного календаря ученые обнаруживают в ряде археологических источников, найденных на огромной территории Евразии. Навыками счета времени на основе изменений положения Луны на ночном небе владели люди, жившие, возможно, в конце позднего палеолита.

Лунные календарные системы стали складываться у разных народов в условиях формирования у них государств. Принято считать, что лунный календарь был создан в Древнем Вавилоне примерно в середине третьего тысячелетия до н.э. Лунным календарем пользовались также в Древнем Китае, Иудее, Древней Греции, Древнем Риме.

Лунные календари учитывают три единицы счета времени: сутки, месяц и лунный год, который представлял собой условную величину, не имеющую астрономического аналога. При построении лунного календаря важно приурочивать начала каждого месяца к новолунию.

Астрономической основой лунных календарей стали два показателя — продолжительность суток и синодического месяца. От одного новолуния до другого проходит 29,53058812 суток = 29 дней 12 часов 44 минуты 2,8 секунды. Лунный год состоит из 12 синодических месяцев общей продолжительностью 354,36706 суток.

Таким образом, синодический месяц не соизмерим ни с сутками, ни с тропическим годом: он не состоит из целого числа суток и не укладывается без остатка в календарном году. Но в календаре должно быть целое число суток, поэтому лунный календарь строится так: основная астрономическая единица счета времени — месяц — округляется до 29 или 30 суток, и с учетом этого календарный лунный год продолжается 354 суток (29 суток х 6 месяцев) + (30 суток х 6 месяцев) = 354 суток. Поскольку начало календарного лунного месяца должно быть как можно ближе к новолунию или совпадать с ним, в течение лунного года должны чередоваться месяцы разной продолжительности. Поэтому обычно все нечетные месяцы содержат по 30, а четные — по 29 дней.

Выстроенный таким образом календарь неизбежно выходит ошибочным против своего астрономического прообраза. Если считать продолжительность календарного лунного года в 354 суток, то ошибка будет равна 0,36706 суток (354,36706 - 354). За три года в результате разницы в продолжительности лунного календарного года и синодического года ошибка составит больше суток (т.е. 3 года х 0,36706 = 1,10118 суток), а в четвертом от начала счета году новолуния будут уже приходиться не на первые, а на вторые числа месяцев, через 8 лет на четвертые и т.д. Быстро накапливаясь, эта ошибка далеко уводила календарные даты от реальных астрономических явлений.

Таким образом, лунный календарь далек от совершенства, и, чтобы согласовать астрономические явления и лунный календарь, время от времени его необходимо поправлять: приблизительно через каждые три лунных года делать вставку в один день, т.е. вместо 354 дней считать в году 355 дней. Лунный год в 354 дня называется простым, а лунный год в 355 дней — продолженным, или високосным.

Учитывая сказанное выше, задача построения лунного календаря сводится к поиску порядка чередования простых и високосных лунных годов, при котором начала календарных месяцев не отодвигались бы заметно от новолуния. Ее решение начинается с поиска такого целого числа лунных лет, составляющего цикл, за которое набегает какое-то целое (или почти целое) число вставных дней. Это найденное число вставных дней и распределяется между отдельными годами внутри цикла.

Уже в древности было предложено много вариантов решения поставленной проблемы. Наиболее известны два варианта поправок лунных календарей.

Один вариант называется турецким циклом, продолжающимся 8 лет. Новолуние в нем опаздывает на трое суток (0,36706 x 8 = = 2,93648). Чтобы этого не допустить, на протяжении 8-летнего цикла вставки делаются трижды. Продолженными годами являются 2-й, 5-й и 7-й годы турецкого цикла. Через 8 лет фазы Луны приходятся на те же самые дни.

Однако и в этом цикле есть ошибка, которая составляет 0,0635 суток, т.е. (354,36706x8) - (354x8) = 0,0635, и фазы Луны по отношению к датам календаря смещаются на 1 сутки назад за 125 лет. Исправить положение можно тем, что через каждые 125 лет один продолженный год в 8-летнем цикле, например 7-й, оставлять простым.

Второй вариант исправления лунного календаря с помощью високосов представлен в арабском цикле. Цикл состоит из 30 лет, в котором 19 простых и 11 продолженных лет. Продолженными являются 2, 5, 7, 10, 13, 16, 18, 21, 24, 26 и 29-й годы цикла. Погрешность этого цикла дает сдвиг в 1 сутки относительно первых чисел календарных месяцев примерно за 2500 лет.

Сегодня лунный календарь используется у исламских народов, в том числе и у некоторых народов, проживающих на территории Российской Федерации и исповедующих ислам. Этот календарь еще называют мусульманским или лунной хиджрой.

Перевод дат с мусульманского календаря на солнечный календарь. Даты календаря лунной хиджры переводятся на григорианский календарь с помощью формулы:

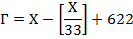
где Г — год григорианского календаря; X — год хиджры.

Символ [] в формулах означает, что для расчетов берется только целая часть частного.

Если требуется определить, какому году календаря лунной хиджры соответствует данный год григорианского календаря, пользуются формулой

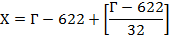
При переводе дат по этим формулам может возникнуть неточность, равная одному году.

При необходимости получить более точные переводы на солнечный, в частности юлианский, календарь не только года, но и других элементов дат пользуются специальными формулами и таблицами.

Алгоритм операций, необходимых для перевода дат мусульманского календаря (с арабским вариантом чередования продолженных годов) на юлианский, следующий.

Устанавливается число полных 30-летних циклов п и полных лет текущего цикла т:

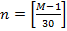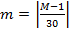
где М — номер года лунной хиджры. Символ | | означает, что для дальнейших расчетов берется лишь целый остаток от деления.

Устанавливается, сколько дней D прошло во всех полных 30-летних циклах от начала эры хиджры:

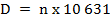так как в полном 30-летии насчитывается 10 631 день, и это значение постоянно.

Устанавливается число дней Д в прошедших годах текущего 30-летия:

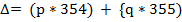где р и q — число прошедших простых и високосных лет соответственно, и их количество устанавливается от начала чередования простых и продолженных лет в арабском цикле (см. выше). Очевидно, что .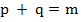

Устанавливается, сколько дней N прошло от начала мусульманского года (1 Мухаррама) до заданной даты, включая ее:

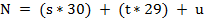где s и t — соответственно число полных (по 30 дней) и пустых (по 29 дней) истекших месяцев, и — число дней в текущем месяце, включая определяемую дату.

Число полных и пустых месяцев определяем по таблице месяцев мусульманского календаря (табл. 1).

Таблица 1. Месяцы мусульманского календаря

Порядковый номер месяца	Название месяца	Число дней
	Мухаррам
	Сафар
	Раби аль-авваль(Раби 1)
	Раби ас-сани (Раби II)
	Джумада аль-уля (Джумада I)
	Джумада аль-ахира (Джумада II)
	Раджаб
	Шаабан
	Рамадан
	Шаввал
	Зу-л-Каада
	Зу-л-Хиджа

5. Подсчитывается, сколько дней Z прошло от начала н.э. до интересующей нас даты (от начала н.э. до эпохи хиджры их прошло 227 016, и это постоянное значение):

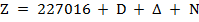Устанавливается число истекших от начала н.э. полных четырехлетних юлианских циклов J (1461 день, это постоянное значение) и число дней в неполном цикле В:

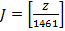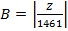
Очевидно, что число юлианских лет в этих полных четырехлетних циклах составит 4 J.

Определяется число полных годов К в текущем четырехлетии и число дней в текущем году d:

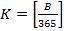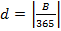
Устанавливается номер года н.э.:

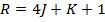
В табл. 2 «Порядковый счет дней в году» отыскивается число месяца юлианского календаря в текущем году, иначе говоря, соотносится значение d с числом и месяцем, указанным в таблице.

Таблица 2.Порядковый счет дней в году

Число

Месяц

VII

VIII

XII