2015-06-14
432
Уровни динамического ряда зависят от одного факторного признака – времени. Поэтому рассмотрим характеристики, описывающие свойства ряда в зависимости от этого признака.
1). Коэффициент корреляции является оценкой силы линейной связи между уровнями ряда и временем (датой).
Выборочный коэффициент корреляции вычисляется по формуле
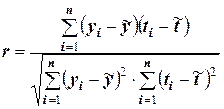
Здесь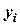 
- уровень ряда (значение курса валюты) в i -й период (день); 
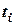- дата i -го периода; 
. 
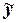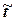- средние значения уровней ряда и даты соответственно.
2). Проверить наличие тенденции можно и другим способом. Разобьем динамический рад на две равные части. Вычислим средние значения для каждой из частей. Проверим гипотезу о равенстве средних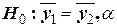 
. Здесь 
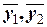- генеральные средние первого и второго полупериодов (частей) динамического ряда; 
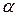- уровень значимости. Если гипотеза не отклоняется, то это означает, что генеральное среднее первой части динамического ряда незначимо отличается от генерального среднего второй. То есть уровни динамического ряда не имеют тенденции к стабильному изменению. В противном случае, при отклонении гипотезы, можно утверждать, что существует устойчивая тенденция к изменению уровней ряда. О направлении изменения можно догадаться, сравнив выборочные средние 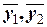. Если 
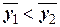, то уровни ряда в среднем растут. При противоположном знаке неравенства – убывают.
3). Уравнение регрессии описывает аналитическую зависимость среднего значения уровней ряда от времени. Именно с помощью регрессионного анализа можно прогнозировать значения уровней динамического ряда в будущем. И именно эти прогнозные значения необходимо знать, чтобы оценить доходность валютных вкладов.
