Обозначим точность выборки приближенного равенства 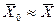 буквой e. Тогда определение точности вычисления генерального среднего значения по данным выборки сводится к определению вероятности a — вероятности того, что истинное значение
буквой e. Тогда определение точности вычисления генерального среднего значения по данным выборки сводится к определению вероятности a — вероятности того, что истинное значение 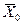 находится в переделах
находится в переделах 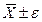 , т.е.
, т.е.
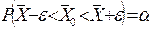
Для определения вероятности a пользуются распределением величины t:
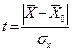
Распределение величины t называется распределением Стьюдента.
Известно, что
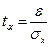
где ta — величина t, соответсвующая определенной вероятности a зависящая от числа степеней свободы k = n-1 (n — объем выборки).
Величина ta приводиться в таблицах справочников по прикладной статистике. При помощи этой таблицы можно определить одно из трех значений: вероятность a, точность e или объем выборки n, задаваясь предварительно значениями каких-либо двух из этих величин.
Пример. По выборке объема n = 15 найдено 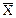 = 20,4 и s = 0,8. Определить, в каком диапазоне находится истинное значение генеральной средней
= 20,4 и s = 0,8. Определить, в каком диапазоне находится истинное значение генеральной средней 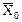 .
.
Генеральная средняя определяется доверительными границами
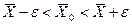 ,
,
где
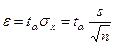
Зададимся точностью a = 0,98, тогда по таблице при k = n-1 = 14 находим
ta = 2,62
Поэтому
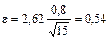
Следовательно,
(20,4 - 0,54) < 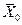 < (20,4 + 0,54)
< (20,4 + 0,54)
19,86 < 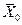 < 20,94
< 20,94
Пример. Определить, какой должен быть объем выборки n, если необходимо вычислить 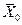 с вероятностью a = 0,95 и точностью e = 0,1s.
с вероятностью a = 0,95 и точностью e = 0,1s.
Так как
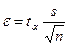 ,
,
то
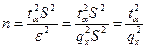
По таблицам для a = 0,95 ta = 1,96, и представив e = qхs, получаем qх = 0,1.
Тогда
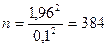
Таким образом, объем выборки должен быть 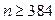 .
.
 2015-06-04
2015-06-04 1310
1310
