2015-06-04
609
Пусть имеем квадратную матрицу
и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:
1. Найти определитель матрицы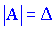 
. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
2. Найти алгебраические дополнения элементов матрицы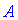 
. Они равны минорам, умноженным на 
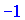в степени суммы строки и столбца, для которого ищем.
3. Составить матрицу из алгебраических дополнений элементов матрицы 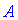матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается 
.
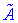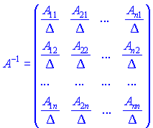
4. Разделить присоединенную матрицу на детерминант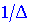 
. Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
