2015-06-04
8463
Исторический обзор обоснований геометрии. “Начала” Евклида. Элементы геометрии Лобачевского. Общие вопросы аксиоматики. Требования к системам аксиом: полнота, независимость, непротиворечивость. Системы аксиом Вейля евклидова пространства.
Исторический обзор обоснований геометрии:
Основным методом современной математики, в частности геометрии, является аксиоматический метод, который берет свое начало от “Оснований геометрии” Д. Гильберта. Геометрия, прежде чем стать аксиоматической теорией, прошла долгий путь эмпирического развития.
Первые сведения о геометрии были получены цивилизациями Древнего Востока – в Египте, Китае, Индии – в связи с развитием земледелия, ограниченностью плодородных земель и др. В этих странах геометрия носила эмпирический характер и представляла собой набор отдельных “рецептов-правил” для решения конкретных задач. Уже во II тыс. до н.э. египтяне умели точно вычислять площадь треугольника, объем усеченной пирамиды, площадь круга, а вавилоняне знали теорему Пифагора. Заметим, что доказательств не было, а указывались лишь правила для вычислений.
Греческий период развития геометрии начался в VII–VI вв. до н. э. под влиянием египтян. Отцом греческой математики считается знаменитый философ Фолес (640–548 до н.э.). Фолесу, точнее его математической школе, принадлежат доказательства свойств равнобедренного треугольника, вертикальных углов. В дальнейшем им были получены результаты, охватывающие почти все содержание современного школьного курса геометрии.
Философская школа Пифагора (570–471 до н.э.) открыла теорему о сумме углов треугольника, доказала теорему Пифагора, установила существование пяти типов правильных многогранников и несоизмеримых отрезков, Демокрит (470–370 до н.э.) открыл теоремы об объемах пирамиды и конуса. Евдокс (410–356 до н.э.) создал геометрическую теорию пропорций (т. е. теорию пропорциональных чисел). Менехм (IV в. до н.э.) и Аполлоний Пергский (2-я пол. III в. – 1-я пол. II в. до н.э.) создали теорию конических сечений. Архимед (289–212 до н.э.) открыл правила вычисления площади поверхности и объема шара и других фигур. Он же нашел приближенное значение числа p.
Особая заслуга древнегреческих ученых состоит в том, что они первыми поставили проблему строгого построения геометрических знаний и решили ее в первом приближении. Проблему поставил Платон (428–348 до н.э.). Аристотелю (384–322 до н.э.) – крупнейшему философу, основателю формальной логики – принадлежит четкое оформление идеи построения геометрии в виде цепи предложений, которые вытекают одно из другого на основе лишь правил логики.
Эту задачу пытались решить многие греческие ученые (Гиппократ, Федий). Воспитанник школы Платона, крупнейший геометр древности Евклид (330–275 до н.э.), живший в Египте (в Александрии), является автором 13 книг (глав) под названием “Начала”. В них он дает систематическое изложение начал геометрии на таком научном уровне, что многие века преподавание геометрии велось по его сочинению. Первые шесть книг (I–VI) посвящены планиметрии; книги VII–IX – арифметике в геометрическом изложении; X – несоизмеримым отрезкам, и XI–XIII – стереометрии.
Замечание 1. В “Начала” были включены не все сведения, известные в геометрии. Например, в эти книги не вошла теория конических сечений, а также кривые высших порядков.
Замечание 2. Каждая книга начинается с определения тех понятий, которые в ней встречаются. Например, в книге II даны 23 определения. Приведем определения первых четырех понятий:
1. Точка есть то, что не имеет частей.
2. Линия есть длина без ширины.
3. Границы линии суть точки.
4. Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам.
Евклид приводит предложения, принимаемые без доказательства, разделяя их на постулаты и аксиомы. Постулатов у него пять, а аксиом – семь. Вот некоторые из них.
Постулаты
<...> IV. И чтобы все прямые углы были равны.
V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
Аксиомы
I. Равные порознь третьему равны между собой.
II. И если к равным прибавить равные, то получим равные.
<...> VII. И совмещающиеся равны.
Замечание 1. Евклид не указал, в чем заключается различие между постулатами и аксиомами. До сих пор нет окончательного решения этого вопроса.
Замечание 2. Евклид изложил теорию геометрии так, как требовали греческие ученые, особенно Аристотель, т.е. теоремы расположены таким образом, что каждая следующая доказывается только на основе предыдущих. Иначе говоря, Евклид, развивая геометрическую теорию, придерживается строго логического пути. В этом и заключается историческая заслуга Евклида перед наукой.
“Начала” Евклида сыграли огромную роль в истории математики и всей человеческой культуры. Эти книги переведены на все основные языки мира, после 1482 г. они выдержали около 500 изданий.
Недостатки системы Евклида. С точки зрения современной математики изложение “Начал” следует признать несовершенным. Назовем основные недостатки этой системы:
1. Многие понятия включают такие, которые в свою очередь требуют также определения (например, используемые в определениях 14 главы 1 понятия ширины, длины, границы).
2. Список аксиом и постулатов недостаточен для построения геометрии строго логическим путем. Например, в этом списке нет аксиом порядка, без которых нельзя доказать многие теоремы геометрии (на это обстоятельство обратил внимание Гаусс). В указанном списке отсутствуют также определения понятия движения (совмещения) и свойств движения, т.е. аксиом движения. В списке нет также аксиомы Архимеда (одной из двух аксиом непрерывности), которая играет важную роль в теории измерений длин отрезков, площадей фигур и объектов тел. Заметим, что на это обратил внимание современник Евклида – Архимед.
3. Постулат IV явно лишний, его можно доказать как теорему.
Особо отметим постулат V, В книге I “Начал” первые 28 предложений доказаны без ссылок на него. Попытка минимизировать список аксиом и постулатов, в частности доказать постулат V как теорему, проводилась со времен самого Евклида. Прокл (V в. н. э.), Омар Хайям (1048-1123), Валлис (XVII в.), Саккери и Ламберт (XVIII в.), Лежандр (1752–1833) также пытались доказать постулат V как теорему. Их доказательства были ошибочными, но они привели к положительным результатам – рождению еще двух геометрий (Римана и Лобачевского).
Неевклидовы геометрические системы. Н.И. Лобачевский (1792–1856), который открыл новую геометрию – геометрию Лобачевского, также начал с попытки доказательства постулата V. Он развил свою систему до объема “Начал” в надежде получить противоречие. Не получил, но сделал (1826) правильный вывод: существует геометрия, отличная от геометрии Евклида.
На первый взгляд этот вывод кажется недостаточно обоснованным: может быть, развивая его дальше, можно прийти к противоречию. Но этот же вопрос относится и к геометрии Евклида. Иначе говоря, обе геометрии равноправны перед вопросом о логической непротиворечивости. Дальнейшие исследования показали, что из непротиворечивости одной следует непротиворечивость другой геометрии, т. е. имеет место равноправие логических систем.
Лобачевский был первым, но не единственным, сделавшим вывод о существовании другой геометрии. Гаусс (1777–1855) высказал эту идею еще в 1816 г. в частных письмах, но в официальных публикациях заявление не сделал.
Три года спустя после публикации результатов Лобачевского (1829), т.е. в 1832 г., вышла работа венгра Я. Бойяи (1802–1860), который в 1823 г. пришел к выводу о существовании другой геометрии, но опубликовал его (вывод) позже и в менее развитом, чем у Лобачевского, виде. Поэтому справедливо, что эта геометрия носит имя Лобачевского.
Общему признанию геометрии Лобачевского в значительной степени способствовали последующие работы математиков. В 1868 г. итальянский математик Э. Бельтрами (1825–1900) доказал, что на поверхности постоянной отрицательной кривизны (так называемая псевдосфера) подтверждается геометрия Лобачевского. Уязвимым местом доказательства непротиворечивости геометрии Лобачевского, основанного на интерпретации Бельтрами, было то, что, как показал Гильберт (1862–1943), в евклидовом пространстве не существует полной поверхности постоянной отрицательной кривизны без особенностей. Поэтому для поверхности постоянной отрицательной кривизны можно интерпретировать только часть плоской геометрии Лобачевского. Этот недостаток был устранен позднее Пуанкаре (1854–1912) и Клейном (1849–1925).
Доказательство непротиворечивости геометрии Лобачевского было вместе с тем и доказательством независимости постулата V от остальных. Действительно, в случае зависимости геометрия Лобачевского была бы противоречивой, так как она содержала бы два взаимно исключающих утверждения.
Дальнейшие исследования евклидовой геометрии подтвердили неполноту системы аксиом и постулатов Евклида. Исследование аксиоматики Евклида завершил в 1899 г. Гильберт, аксиоматика которого состоит из пяти аксиом, а именно:
• связи (принадлежности);
• порядка;
• конгруэнтности (равенства, совпадения);
• непрерывности;
• параллельности.
Эти аксиомы (всего их 20) относятся к объектам трех родов: точки, прямые, плоскости, а также к трем отношениям между ними, выражаемыми словами: “принадлежит”, “лежит между”, “конгруэнтен”. Конкретный смысл точек, прямых, плоскостей и отношений не указан. Они косвенно определены через аксиомы. Благодаря этому построенная на основе аксиом Гильберта геометрия допускает различные конкретные реализации.
Геометрическая система, построенная на перечисленных аксиомах, называется евклидовой, так как совпадает с геометрией, изложенной Евклидом в “Началах”.
Геометрические системы, отличные от евклидовой, называются неевклидовыми геометриями. Согласно общей теории относительности, в пространстве ни та, ни другая не являются абсолютно точными, однако в малых масштабах (земные масштабы являются также достаточно малыми) они вполне пригодны для описания пространства. Применение на практике евклидовых формул объясняется их простотой.
Гильберт всесторонне исследовал свою систему аксиом, показал, что она непротиворечива, если не противоречива арифметика (т.е. на самом деле доказана содержательная или так называемая внешняя непротиворечивость). Он завершил многовековые исследования ученых по обоснованию геометрии. Эта работа была высоко оценена и в 1903 г. отмечена премией имени Лобачевского.
В современном аксиоматическом изложении геометрии Евклида не всегда пользуются аксиомами Гильберта: учебники по геометрии построены на различных модификациях этой системы аксиом.
В XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики как одна из возможных геометрий, но и непосредственно связана с приложениями математики. Оказалось, что взаимосвязь пространства и времени, открытая А. Эйнштейном и другими учеными в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского.
“Начала” Евклида:
«Начала» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии. «Начала» — вершина античной геометрии и античной математики вообще, итог её 300-летнего развития и основа для последующих исследований. «Начала», наряду с двумя трудами Автолика из Питаны — древнейшее из дошедших до нас античных математических сочинений; все труды предшественников Евклида известны нам только по упоминаниям и цитатам позднейших комментаторов.
Прокл сообщает (ссылаясь на Евдема), что подобные сочинения создавались и до Евклида: «Начала» были написаны Гиппократом Хиосским, а также платониками Леонтом и Февдием. Но эти сочинения, по-видимому, были утрачены ещё в античности.
Текст «Начал» на протяжении веков были предметом дискуссий, к ним написаны многочисленные комментарии. Из античных комментариев до нас дошёл комментарий, написанный Проклом[1]. Этот текст является важнейшим источником по истории и методологии греческой математики. Прокл дает краткое изложение истории греческой математики (т. н. Евдемов каталог геометров), обсуждает взаимосвязь метода Евклида и логики Аристотеля, роль воображения в доказательствах.
Из древних комментаторов следует упомянуть Паппа, из новых — Пьера Рамуса[2], Федериго Коммандино[3], Христофа Шлюсселя (Клавиуса)[4] и Савилия.
«Начала» оказали огромное влияние на развитие математики вплоть до Новейшего времени. Книга переведена на множество языков мира. По количеству переизданий «Начала» не имеют себе равных среди светских книг.
Альберт Эйнштейн так оценивал «Начала»: «Это удивительнейшее произведение мысли дало человеческому разуму ту уверенность в себе, которая была необходима для его последующей деятельности. Тот не рождён для теоретических исследований, кто в молодости не восхищался этим творением»
В «Началах» излагаются планиметрия, стереометрия, арифметика, отношения по Евдоксу. В классической реконструкции Гейбергавесь труд состоит из 13 книг. К ним традиционно присоединяют две книги о пяти правильных многогранниках, приписываемые Гипсиклу Александрийскому и школе Исидора Милетского.
Изложение в «Началах» ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, например, I def. 2 — второе определение первой книги.
Элементы геометрии Лобачевского:
Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется на аксиому о параллельных прямых Лобачевского.
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:
| Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её. |
В геометрии Лобачевского, вместо неё принимается следующая аксиома:
| Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. |
Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются[1]. Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитиигеометрии, математики и науки вообще.
Общие вопросы аксиоматики:
общепринятая аксиоматика для математического описания теории вероятностей. Первоначальный вариант предложен Андреем Николаевичем Колмогоровым[1][2] в 1929 году, окончательная версия — в 1933 году. Аксиоматика Колмогорова позволила придать теории вероятностей стиль, принятый в современной математике.
Требования к системам аксиом:
Система аксиом называется независимой, если ни одна из аксиом этой системы не зависит от остальных аксиом, т.е. не может быть доказана как теорема с помощью других аксиом данной системы аксиом.
Независимость системы аксиом.
Полнота системы аксиом.
Непротиворечивость системы аксиом
17. Неевклидовы геометрии.
Проблема пятого постулата Евклида. Простейшие факты гиперболической геометрии Н.И. Лобачевского, эллиптической геометрии Б. Римана и сферической геометрии.
Проблема пятого постулата Евклида:
Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основанииклассической планиметрии. Впервые приведена в «Началах» Евклида [1]:
| И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двухпрямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двухпрямых. |
Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал»Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. Вклассическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.
На современном языке текст Евклида можно переформулировать так:
Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении ихтретьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту жесторону от секущей.
Простейшие факты гиперболической геометрии Н.И. Лобачевского, эллиптической геометрии Б. Римана и сферической геометрии:
Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий,геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, заисключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:
Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с даннойпрямой в одной плоскости и не пересекающей её.
В геометрии Лобачевского, вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с даннойпрямой в одной плоскости и не пересекающие её.
Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются[1].Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое ифилософское её значение состоит в том, что её построением Лобачевский показал возможность геометрии,отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.
Римана геометрия
эллиптическая геометрия, одна из неевклидовых геометрий(См. Неевклидовы геометрии), т. е. геометрическая теория, основанная на аксиомах, требования которых (взначительной части) отличны от требований аксиом евклидовой геометрии (См. Евклидова геометрия).Основными объектами, или элементами, трёхмерной Р. г. являются точки, прямые и плоскости; основныепонятия Р. г. суть понятия принадлежности (точки прямой, точки плоскости), порядка (например, порядкаточек на прямой или порядка прямых, проходящих через данную точку в данной плоскости) и конгруэнтности(фигур). Требования аксиом Р. г., касающиеся принадлежности и порядка, полностью совпадают стребованиями аксиом проективной геометрии (См. Проективная геометрия). Соответственно, в Р. г. имеютместо, например, следующие предложения: через каждые две точки проходит одна прямая, каждые двеплоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются(в одной точке), точки на прямой расположены в циклическом порядке (как и прямые, лежащие в однойплоскости и проходящие через одну точку). Требования аксиом Р. г., касающиеся конгруэнтности, сходны стребованиями соответствующих аксиом геометрии: во всяком случае они обеспечивают движения (См.Движение) фигур по плоскости и в пространстве Римана столь же свободные, как на плоскости и впространстве Евклида. Метрические свойства плоскости Римана «в малом» совпадают с метрическимисвойствами обыкновенной сферы. Точнее: для любой точки плоскости Римана существует содержащая этуточку часть плоскости, изометричная некоторой части сферы; радиус R этой сферы — один и тот же для всехплоскостей данного пространства Римана. Число К = 1/ R2 называется кривизной пространства Римана (чемменьше К, тем ближе свойства фигур этого пространства к евклидовым). Свойства плоскости Римана «вцелом» отличаются от свойств целой сферы; так, например, на плоскости Римана две прямые пересекаютсяв одной точке, а на сфере два больших круга, которые играют роль прямых в сферической геометрии,пересекаются в двух точках; прямая, лежащая на плоскости, не разделяет эту плоскость (т. е., если прямая а лежит в плоскости α, то любые две точки плоскости α, не лежащие на прямой а, возможно соединитьотрезком, не пересекая прямой а).
По-видимому, первое сообщение о Р. г. сделано Б. Риманом в его лекции «О гипотезах, лежащих восновании геометрии» (1854, опубликовано в 1867), где Р. г. рассматривалась как частный случай римановойгеометрии (См. Риманова геометрия) — теории римановых пространств (См. Риманово пространство) вшироком смысле. Р. г. относится к теории пространств постоянной положительной кривизны.
18. Многоугольники. Площадь многоугольника. Теорема существования и единственности. Равновеликость и равносоставленность.
Длина отрезка. Ломаная, звенья ломаной, простая ломаная, замкнутая ломаная, простой многоугольник, граница многоугольника, ориентированный многоугольник. Характеристика многоугольника. Площадь многоугольника. Аксиомы измерения площадей. Теорема существования и единственности. Равновеликие и равносоставленные многоугольники
Длина отрезка: отрезок- это часть прямой линии, ограниченная двумя точками - началом и концом.
А длина отрезка это расстояние от одной точки до другой.
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Ломаная, звенья ломаной, простая ломаная, замкнутая ломаная, простой многоугольник, граница многоугольника, ориентированный многоугольник:
Ломаная - геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами.
Составные отрезки ломаной называются ее сторонами или звеньями, а их концы – вершинами ломаной. Наименьшее возможное количество звеньев ломаной – два. Конечные вершины ломаной называются черными точками.
Графически линию обозначают по названиям ее вершин, например, ломаная ABCDEFG. Ломаная линия может быть замкнутой, т.е. ее конечные вершины совпадают. Разновидностями такой линии являются многоугольники. Многоугольник – это плоская замкнутая ломаная, которая не имеет самопересечений. Вершины ломаной называются вершинами многоугольника, а ее звенья – сторонами многоугольника.
Многоугольник с тремя сторонами и вершинами называется треугольником. Замкнутая ломаная с четырьмя сторонами может быть квадратом, прямоугольником, ромбом, параллелограммом, трапецией. Фигура с пятью и более сторонами называется n-угольником, где n – число вершин.
Ломаная линия может иметь самопересечения. Классическим примером замкнутой ломаной с самопересечениями является пятиконечная звезда.
Разновидностью ломаной линии является зигзаг, в котором отрезки параллельны друг другу через один, а последовательные образуют одинаковый угол. Зигзаги используются в швейном деле, а также при декоративном оформлении предметов обихода (посуды, мебели, книг) в качестве орнамента.
Характеристика многоугольника:
Многоуго́льник — это замкнутые ломаные линии, не имеющиесамопересечения.
Последняя фигура, изображенная на рисунке не является многоугольником, так как несмежные отрезки имеют более одной общей точки.
Существуют три различных варианта определения многоугольника:
· Плоская замкнутая ломаная — самый общий случай;
· Плоская замкнутая ломаная без самопересечений — простой многоугольник;
· Часть плоскости, ограниченная замкнутой ломаной без самопересечений.
В любом случае, вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Площадь многоугольника:
Формула для нахождения площади правильного многоугольника:Площадь = 1/2 х периметр х апофема.
· Периметр - сумма сторон многоугольника.
· Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
Аксиомы площади:
Теорема существования и единственности:
Теорема существования — утверждение, которое устанавливает, при каких условиях существует решение математической задачи или математический объект, например производная, неопределенный интеграл, определенный интеграл, решение уравнения и т. д. При доказательстве теорем существования используются сведения из теории множеств. Теоремы существования играют очень важную роль в различных приложениях математики, например при математическом моделировании различных явлений и процессов. Математическая модель не адекватна конкретному описываемому явлению, из существования решения реальной задачи не следует существование соответствующей математической задачи. Доказательство теорем существования необходимо перед решением различных математических задач, вроде вычисления интеграла или интегрирования дифференциального уравнения. Теоремы существования позволяют определить, существует ли вычисляемый интеграл и сколько решений имеет дифференциальное уравнение. Если удается доказать теорему существования, единственность решения и корректность самой постановки задачи, то это означает очень важный первый шаг в решении задачи.
Равновеликие и равносоставленные многоугольники:
При вычислении площадей многоугольников используется простой прием, называемый методом разбиения. Рассмотрим многоугольник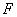и 
и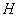 
, изображенные на рис. 1, где показано, как разбить эти многоугольники на одинаковое число соответственно равных частей (равные части отмечены одинаковыми цифрами). О многоугольниках 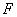и 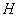говорят, что они равносоставлены. Вообще, многоугольник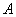и 
и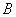 
называются равносоставленными, если, определенным образом разрезав многоугольник 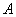на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник 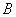. Легко видеть, что справедлива следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, или, как говорят, равновелики. Например,параллелограмм равносоставлен с прямоугольником (рис. 2), и потому, зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты.
Рис. 1
Рис. 2
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна. Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту (рис. 3); из этого легко выводится формулаплощади треугольника. Этот способ вычисления площадей многоугольников был известен еще Евклиду, который жил более 2000 лет назад.
