Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 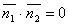или .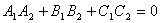

Таким образом, .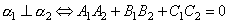

Условия параллельности 2х плоскостей. Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы 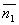и 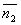параллельны, а значит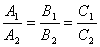

Угол между прямыми в пространстве:

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

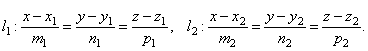
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторам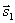и и 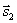. Так как 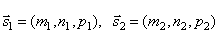, то по формуле для косинуса угла между векторами получим

.

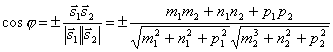Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 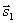и :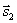

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l ₁ параллельна l ₂ тогда и только тогда, когда 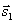параллелен .

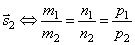Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .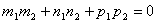

Угол между прямой и плоскостью:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу