Условия параллельности и перпендикулярности прямой и плоскости в пространстве

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

9. Поверхности второго порядка.

Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

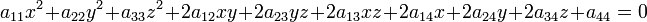
в котором по крайней мере один из коэффициентов 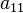, , 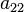, , 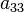, 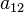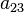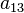отличен от нуля.

Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси.

Цилиндрическая поверхность — поверхность второго порядка, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению. В декартовых координатах может быть выражена уравнениями: 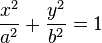; ; 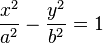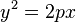, и некоторыми другими.

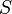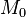Конические поверхности: Поверхность называется конической поверхностью с вершиной в точке , если для любой точки этой поверхности прямая, проходящая через 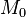и 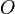, целиком принадлежит этой поверхности.

Функция 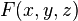называется однородной порядка 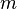, если 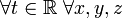выполняется следующее: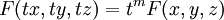

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность 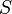задана уравнением 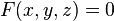, где 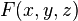— однородная функция, то 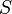— коническая поверхность с вершиной в начале координат.

Если поверхность 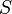задана функцией 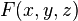, являющейся однородным алгебраическим многочленом второго порядка, то 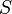называется конической поверхностью второго порядка.

· Каноническое уравнение конуса второго порядка имеет вид:

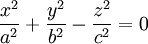
Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:

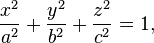где 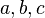— произвольные положительные числа.

Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это вид поверхностивторого порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

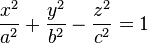(однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

или

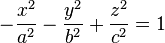(двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может бытьполучен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: 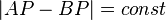. В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

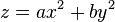
· есл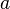и и 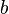одного знака, то параболоид называется эллиптическим.

· есл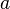и и 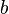разного знака, то параболоид называется гиперболическим.

· если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.

· Эллипти́ческийпараболо́ид — поверхность, задаваемая функцией вида

· .

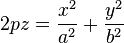· Эллиптический параболоид можно описать как семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх (см. рисунок).

· Если 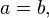то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.

· Гиперболи́ческийпараболо́ид (называемый в строительстве «гипар») — седловая поверхность, описываемая в прямоугольной системе координат уравнением вида

· .

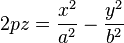· Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх (см. рисунок).

· Гиперболический параболоид является линейчатой поверхностью.