2015-06-04
849
Для этого представим уравнения (1) - (3) в виде системы дифференциальных уравнений, где оператор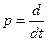 
обозначает 1-ую производную.
Кроме того, определим понятие «переменные», представляющие собой реальные воздействия, и, при этом, изменяющиеся в зависимости от поставленной перед собой задачи.
Выберем переменные, которые будем считать «входами» (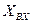
), и переменные, которые будем считать «выходами» (
).
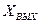В одной из очевидных постановок задачи входными переменными будут являться вращающий электромагнитный момент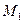 
, который формируется с помощью ЭД, а также моменты сопротивлени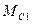й 
и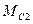 
, создаваемые, в основном, силами трения. Выходной переменной будет являться скорость второй массы 
.
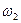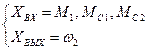
Продифференцируем уравнение (1):
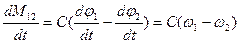
Тогда введя понятие «оператор», можно представить уравнения (1) - (3) в операторной форме:
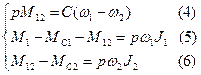
Решение задачи сводится к представлению графического образа системы, который состоит из совокупности графических образов отдельных звеньев и в них содержатся переменные (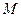
, 
, 
, 
, 
, 
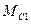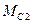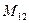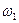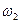), параметры (
, 
, 
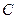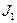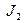) и оператор (
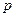). Условимся обозначать переменные стрелками; параметры и оператор, образующие алгебраические выражения заключать в прямоугольные рамки; а для алгебраического суммирования использовать окружности, иногда с секторами, при этом слагаемые обозначаются стрелками подходящими к не заштрихованным секторам окружности, вычитаемые - стрелками подходящими к заштрихованным секторам окружности, а сумму - стрелками отходящими от окружности.
Представим модель согласно уравнению (4).
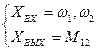
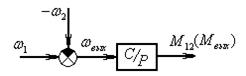
Рис.3а Динамическая модель (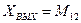
)
Модель, согласно уравнению (5):
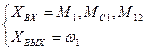
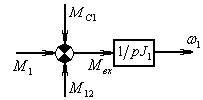
Рис.3б Динамическая модель (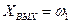
)
Модель, согласно уравнению (6):
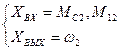
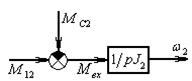
Рис.3в Динамическая модель (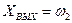
)
В графических образах все выражения, записанные в прямоугольных рамках, представляют собой выражения вида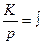 
(интегратор). Поэтому все три представленных звена можно отнести к звеньям интегрирующего типа. Для решения поставленный задачи объединим графические звенья в один графический образ - структурную схему системы. Для этого введем ещё одно обозначение - узел, который будем обозначать точкой, при этом, отходящие от одного узла стрелки соответствуют одной и той же переменной.
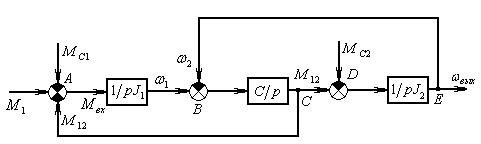
Рис.4 Структурная схема двухмассовой механическойсистемы в переменных «входы-выходы»
Выражение, заключённое в прямоугольные рамки, представляет собой отношение выходной величины к входной, и называется передаточной функцией звена.
Поставим перед собой задачу нахождения общей передаточной функции системы.
Для этого используют операцию агрегирования, т.е. свёртывания структурной схемы с целью представления её в виде одного звена.
