1. Объединением (суммой двух множеств) двух множеств А и В называется новое множество С, которое обозначается С=А 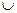 В и содержит элементы, принадлежащие как А, так и В. А
В и содержит элементы, принадлежащие как А, так и В. А 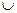 В={х, х
В={х, х 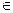 А, х
А, х 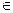 В}
В}
 |
А  В
В 
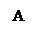
Диаграммы такого вида называются диаграммами Эйлера-Венна
войства:
пределенияоперации изображаются следующим образом:
2.  Пересечением двух множеств А и В называется новое множество С=А
Пересечением двух множеств А и В называется новое множество С=А  В, которое содержит элементы, принадлежащие одновременно и А и В. А
В, которое содержит элементы, принадлежащие одновременно и А и В. А 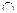 В={х, х
В={х, х 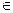 А
А 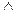 х
х 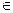 В}
В}
А 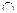 В
В
3. Разностью двух множеств называют новое множество С=А\В которое содержащее элементы, принадлежащие А, но не принадлежащие В. А\В={х,х 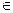 А
А 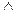 х
х 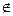 В}
В}
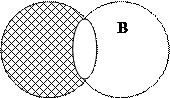
А\В
4. Симметрической разностью называют новое множество С, которое обозначается А 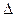 В. Состоит из элементов принадлежащих только А или только В. С={х, х
В. Состоит из элементов принадлежащих только А или только В. С={х, х 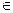 А
А 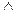 х
х 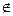 В
В 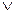 х
х 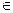 В
В 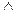 х
х 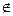 А}
А}
 |
А 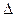 В
В
Свойства:
А 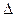 В= А\В
В= А\В 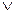 В\А
В\А
А 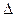 В= (А
В= (А 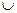 В)\(А
В)\(А 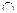 В)
В)
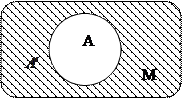
5. Дополнением к множеству А до множества М называется множество, состоящее из элементов, принадлежащих М, но не принадлежащих А, обозначается 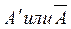
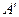 =={х, х
=={х, х 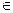 М
М 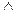 х
х 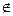 А}. Справедливо:
А}. Справедливо: 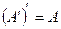
 |
6. Декартовым произведением двух множеств называется новое множество С=А х В, элементы которого представляют собой упорядоченные пары, из которых 1-й элемент принадлежит первому множеству, а 2-й – второму.
Пусть А= {a1, a2} B= {b1, b2}, тогда
А х В= {{a1; в1}, {a2, в2},{a1, в2}, {a2, в1}}
 2015-06-04
2015-06-04 586
586








