2015-06-04
521
Определение. Пусть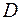 
произвольной подмножество действительных чисел. Однозначной числовой функцией 
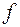, определенной на множестве называется закон, по которому каждому числу 
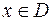поставлено в соответствие одно действительное число 
.
Множество 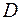при этом называется областью определения функции, а множество 
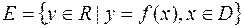— множеством значений функции.
В дальнейшем мы будем рассматривать только однозначные функции.
Пусть на некотором множестве 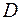определена числовая функция 
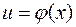и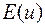 
— множеством значений функции. Пусть на множестве 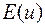задана функция (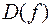
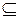
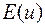). Тогда функция 
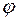отображает элементы 
в элементы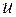 
, а функция 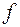отображает элементы 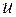в элементы 
,
.
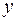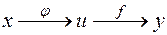
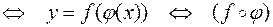Таким образом, в конечном итоге каждому значению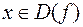 
ставится в соответствие (посредством промежуточной переменной 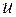) одно определенное значение 
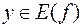, где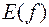 
— множеством значений функции 
.
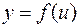В этом случае 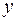называют сложной функцией аргумента или функцией от функции (записывают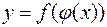 
) или композицией функци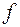й и 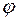(записывают 
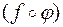). При этом функцию 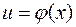называют промежуточным аргументом, — независимой переменной.
|
|
|
Например, функция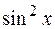 
является сложной. Ее можно записать в виде цепочки равенств:
, 
.
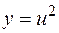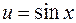Аналогично можно составить сложную функцию с двумя и более промежуточными аргументами. являющуюся композицией более трех функций.
