Теорема. (о единственности предела) Если 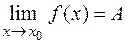 и
и 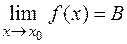 , то
, то 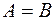 .
.
Доказательство. Предположим, что 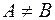 , тогда
, тогда 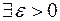 , такое, что пересечение окрестностей
, такое, что пересечение окрестностей 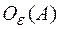 ∩
∩ 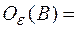 ∅, но с другой стороны для
∅, но с другой стороны для 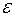
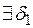 и
и 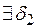 , такие, что
, такие, что
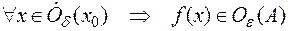 ,
,
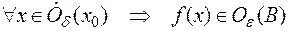 .
.
Но так как пересечение окрестностей равно пустому множеству, то мы получили противоречие.
⊠
Вычисление пределов значительно упрощается, если использовать теоремы о пределах суммы (разности), произведения и частного сходящихся последовательностей.
Теорема. Если функции 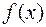 и
и 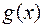 в точке
в точке  имеют конечные пределы, т. е.
имеют конечные пределы, т. е. 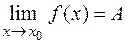 ,
, 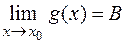 , то:
, то:
1) 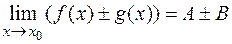 ,
,
2) 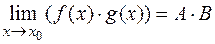 ,
,
3) 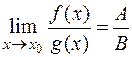
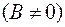 .
.
Теорема(о сравнении функций). Если в 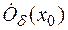
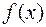 b
b 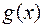 и существуют конечные пределы
и существуют конечные пределы 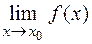 и
и 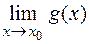 , то
, то
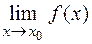 b
b 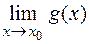 .
.
Теорема. Если в 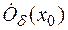
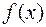 b
b 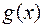 b
b 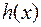 и существуют конечные пределы
и существуют конечные пределы 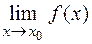
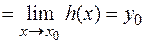 , то и
, то и 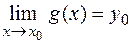 .
.
 2015-06-04
2015-06-04 655
655








