Бесконечно малые и бесконечно большие функции

Определение. Функция 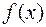называется бесконечно малой функцией (или бесконечно малой) при 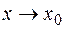, если 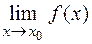= 0 т.е. если для 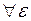>0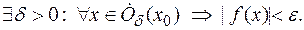

Определение. Функция 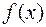называется бесконечно боль­шой функцией (или бесконечно большой) при 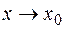, если =¥

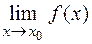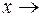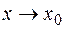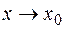Аналогично определяются бесконечно малые функции при ¥, –0, +0.

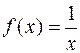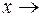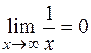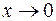Например, функция при ¥ является бесконечно малой, поскольку , при — бесконечно большая, т. к. ¥.

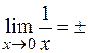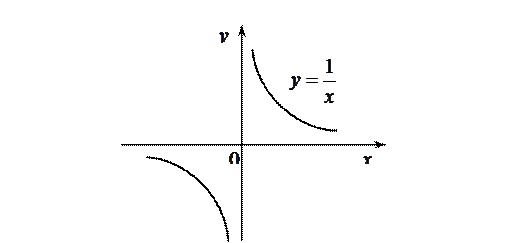
Из приведенного примера следует, что функция, имеющая одно и то же анали­тическое выражение, при разных значениях может быть и бесконечно малой, и бесконечно большой.

Теорема. Если функция 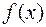при 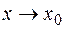— бесконечно большая, то функция 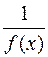при 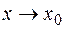— бесконечно малая.

Верно и такое утверждение: если функция 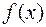при 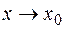— бесконечно малая, то функция 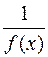при 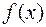—бесконечно большая.

Например, функция 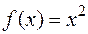при 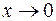является бесконечно малой, то функция 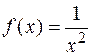при 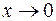— бесконечно большой, т.е.

, ¥.

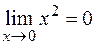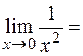Теорема. Конечная сумма бесконечно малых функций в 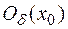есть функция, бесконечно малая в .

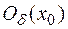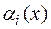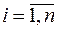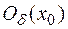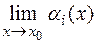Доказательство. Если , —бесконечно малые функции в , то = 0, .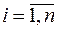

Так как 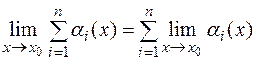= 0,

то конечная сумма бесконечно малых функций действительно есть функция беско­нечно малая.

⊠

Теорема. Произведение бесконечно малой функции и функ­ции, ограниченной в 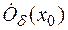, есть бесконечно малая функция.

Следствие 1. Произведение некоторого числа и бесконечно малой функции в 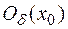есть бесконечно малая функция.

Следствие 2. Произведение двух бесконечно малых функций в 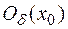есть бесконечно малая функция.

Теорема. Частное от деления бесконечно малой функции 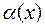в 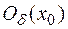на функцию 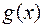, такую, что 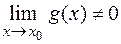, есть беско­нечно малая функция.