Пусть функция  дифференцируема в точке
дифференцируема в точке  , т.е. ее приращение в этой точке представимо в виде
, т.е. ее приращение в этой точке представимо в виде
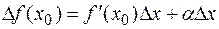 ,
,
где 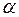 ― бесконечно малая функция при
― бесконечно малая функция при  .
.
Отсюда если 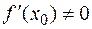 , то
, то
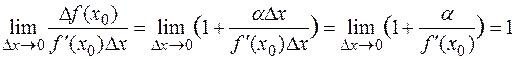 .
.
Следовательно, при 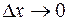 приращение функции
приращение функции 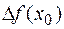 и выражение
и выражение 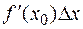 являются эквивалентными бесконечно малыми функциями, т. е. при
являются эквивалентными бесконечно малыми функциями, т. е. при 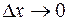 можно приближенно считать, что
можно приближенно считать, что 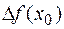 ∼
∼ 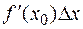 .
.
Определение. Величину 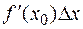 , являющуюся главным (линейным) членом приращения функции
, являющуюся главным (линейным) членом приращения функции  в точке
в точке  , называют дифференциалом функции и обозначают
, называют дифференциалом функции и обозначают 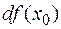 (или
(или 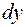 ).
).
Таким образом, по определению
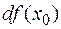 =
= 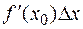 .
.
Найдем дифференциал функции 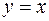 , В этом случае
, В этом случае 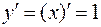 и, следовательно,
и, следовательно, 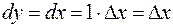 , т. е. дифференциал и приращение независимой переменной равны между собой. Поэтому дифференциал функции
, т. е. дифференциал и приращение независимой переменной равны между собой. Поэтому дифференциал функции  в точке
в точке  можно представить в виде
можно представить в виде
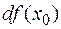 =
= 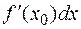 .
.
Следовательно, производную функции можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной:
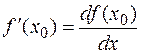 или в более краткой записи
или в более краткой записи 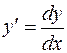 .
.
На рисунке, представленном ниже, дана геометрическая интерпретация дифференциала функции  . Так как
. Так как 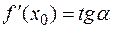 , то дифференциал функции измеряется отрезком
, то дифференциал функции измеряется отрезком 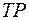 , т. е. дифференциал
, т. е. дифференциал 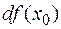 функции
функции  в точке
в точке  изображается приращением ординаты точки касательной, проведенной в
изображается приращением ординаты точки касательной, проведенной в 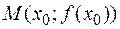 к линии
к линии  .
.
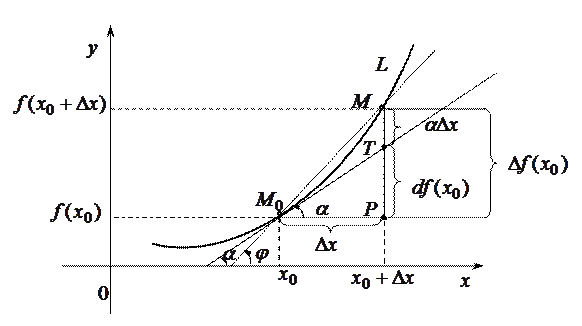
Дифференциал функции можно использовать для вычисления приближенных значений функции. Действительно, заменяя приращение функции в точке  ее дифференциалом, получаем формулу для приближенных вычислений:
ее дифференциалом, получаем формулу для приближенных вычислений:
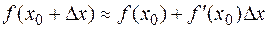 .
.
Пример. Вычислить приближенно 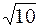 .
.
Решение. Принимая 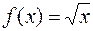 ,
, 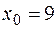 ,
, 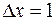 , следовательно,
, следовательно, 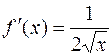 ,
, 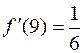 ,
, 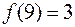 .
.
Тогда: 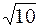
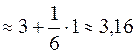 .
.
 2015-06-04
2015-06-04 850
850








