Дифференциал сложной функции

Инвариантность формы диффе­ренциала

Пусть дана сложная функция 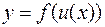. Выше мы определили дифференциал в точке как произведение производ­ной от функции в точке и дифференциала независимой пере­менной:

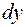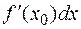= , (1)

В случае сложной функции имеем 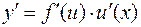, следовательно, 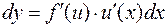. Но так как 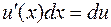, то

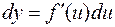. (2)

Формулы (1) и (2) для дифференциала совпадают по форме записи, однако они имеют различный смысл: в первой из них 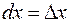, а во второй — .

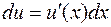В этом и заключается свойство инвариантности формы дифференциала: дифференциал функции всегда равен произве­дению производной и дифференциала аргумента и не зависит от того, является ли величина, по которой взята производная, незави­симой переменной или же только промежуточным аргументом.

Пример. Для функции 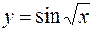найти дифференциал по незави­симой переменной и по промежуточному аргументу.

Решение. 1) Найдем дифференциал по незави­симой переменной

.

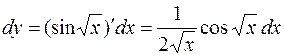2) Найдем дифференциал функции 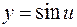по промежуточному аргументу :

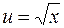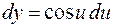или .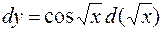

Но так как 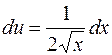полученные результаты в первом и втором случае равны друг другу.