Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Если фиксированное значение аргумента
. Если фиксированное значение аргумента  получает приращение
получает приращение 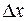 (положительное или отрицательное), такое, что
(положительное или отрицательное), такое, что 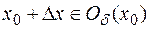 , то приращение функции определяется выражением
, то приращение функции определяется выражением 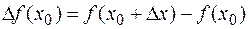 .
.
Определение. Производной функции  в произвольной фиксированной точке
в произвольной фиксированной точке  называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Наиболее употребительные обозначения производной функции:
 в точке
в точке  :
: 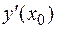 ,
, 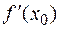 ,
, 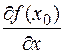 ,
, 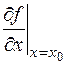 . Таким образом,
. Таким образом,
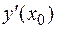
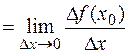
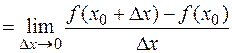
Производная функции  в произвольной точке
в произвольной точке  обозначается так:
обозначается так: 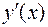 ,
, 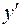 ,
,  ,
, 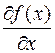 ,
, 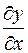 .
.
Операция нахождения производной функции  называется дифференцированием.
называется дифференцированием.
При каждом конкретном числовом значении  производная (если она существует при данном
производная (если она существует при данном  ) функции
) функции  представляет собой определенное число. Значениям переменной
представляет собой определенное число. Значениям переменной  ставятся в соответствие определенные значения переменной
ставятся в соответствие определенные значения переменной  . Следовательно, производная является функцией аргумента
. Следовательно, производная является функцией аргумента  . Можно сказать, что функция
. Можно сказать, что функция  «порождает» (или «производит») функцию
«порождает» (или «производит») функцию  (отсюда и название «производная»).
(отсюда и название «производная»).
|
|
|
Если для некоторого значения 
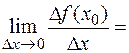 +¥ (или –¥),
+¥ (или –¥),
то говорят, что для этого значения  существует бесконечная производная.
существует бесконечная производная.
В дальнейшем под выражением «функция имеет производную» будем понимать существование конечной производной, если не оговорено противное.
Определение. Если функция  определена в левосторонней (правосторонней) окрестности точки
определена в левосторонней (правосторонней) окрестности точки  и существует конечный или бесконечный предел для этой функции:
и существует конечный или бесконечный предел для этой функции:
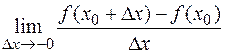
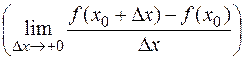 ,
,
то он называется соответственно конечной или бесконечной производной слева (справа) функции  в точке
в точке  и обозначается
и обозначается
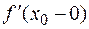
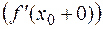 .
.
Левую и правую производные называют односторонними производными. Из свойств пределов следует, что если функция  , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки  , имеет конечную производную
, имеет конечную производную 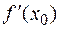 , то существуют производные слева и справа, причем
, то существуют производные слева и справа, причем
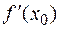 =
= 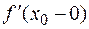 =
= 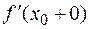
Пример. Найти по определению производную функции 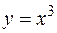 .
.
Решение. Дадим фиксированному значению аргумента  приращение
приращение 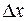 . Тогда:
. Тогда:
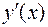
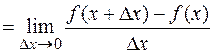
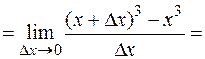
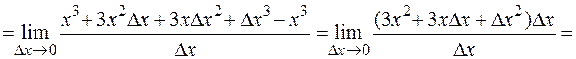
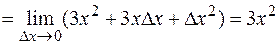 .
.
Механический смысл производной. Рассмотрим функцию  , определенную и непрерывную в некоторой окрестности точки
, определенную и непрерывную в некоторой окрестности точки  . Если аргумент
. Если аргумент  функции получает приращение
функции получает приращение 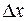 (положительное или отрицательное), такое, что
(положительное или отрицательное), такое, что 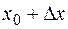 принадлежит той же окрестности точки
принадлежит той же окрестности точки  , то соответствующее приращение функции
, то соответствующее приращение функции 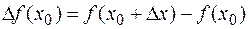 , тогда средняя скорость изменения функции
, тогда средняя скорость изменения функции
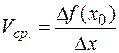 ,
,
а мгновенная скорость ее изменения
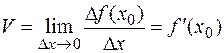 .
.
В этом состоит механический смысл производной, т. е. производная — математическая модель мгновенной скорости процесса, описываемого функцией  . В зависимости от содержательной сущности функции можно получить широкий круг математических моделей скорости протекания процессов. Рассмотрим некоторые из них.
. В зависимости от содержательной сущности функции можно получить широкий круг математических моделей скорости протекания процессов. Рассмотрим некоторые из них.
|
|
|
1. Пусть материальная точка 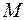 движется неравномерно и
движется неравномерно и 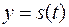 — функция, устанавливающая зависимость пути от времени
— функция, устанавливающая зависимость пути от времени 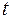 . Тогда мгновенная скорость движения в момент времени
. Тогда мгновенная скорость движения в момент времени 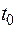 есть производная от пути
есть производная от пути 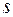 по времени
по времени 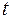 :
:
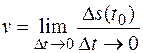 .
.
2. Пусть 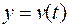 —функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени
—функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени 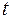 . Тогда мгновенное ускорение материальной точки в фиксированный момент времени
. Тогда мгновенное ускорение материальной точки в фиксированный момент времени 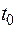 есть производная от скорости
есть производная от скорости 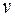 по времени
по времени 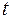 :
:
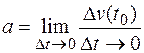 .
.
3. Пусть 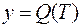 — функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры
— функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры 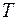 . Тогда теплоемкость тела есть производная от количества теплоты
. Тогда теплоемкость тела есть производная от количества теплоты 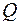 по температуре
по температуре 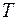 :
:
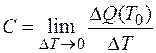 .
.
Геометрический смысл производной. Рассмотрим задачу о проведении касательной к произвольной плоской кривой.
Определение. Касательной к кривой 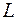 в точке
в точке 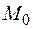 называется прямая
называется прямая 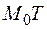 , которая представляет собой предельное положение секущей
, которая представляет собой предельное положение секущей 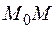 при стремлении по кривой точки
при стремлении по кривой точки 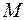 к точке
к точке 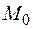 .
.
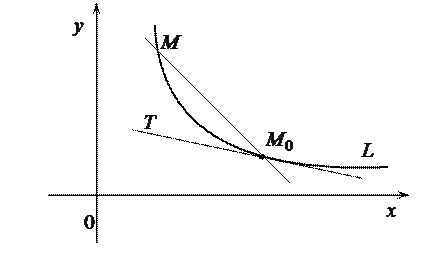
Если предельного положения секущей не существует, то говорят, что в точке 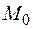 провести касательную нельзя. Это бывает в случае, когда точка
провести касательную нельзя. Это бывает в случае, когда точка 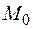 является точкой излома, или заострения, кривой.
является точкой излома, или заострения, кривой.
|

Пусть кривая 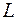 является графиком функции
является графиком функции  и точка
и точка 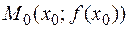
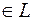 . Предположим, что касательная к кривой в точке
. Предположим, что касательная к кривой в точке 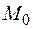 существует. Угловой коэффициент секущей
существует. Угловой коэффициент секущей 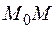
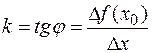 .
.
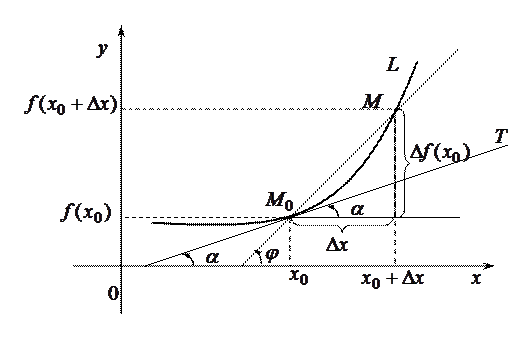
Если 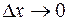 , то точка
, то точка 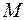 движется по кривой к точке
движется по кривой к точке 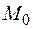 и секущая
и секущая 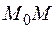 стремится к своему предельному положению
стремится к своему предельному положению 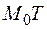 . Таким образом,
. Таким образом,
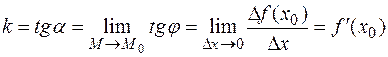 ,
,
т. е. если кривая 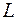 является графиком функции
является графиком функции  , то производная от функции
, то производная от функции  при
при 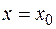 равна угловому коэффициенту касательной к графику функции в точке с абсциссой
равна угловому коэффициенту касательной к графику функции в точке с абсциссой  .
.
Уравнения касательной и нормали. Угол между кривыми. Для составления уравнений касательной и нормали к плоской кривой используем геометрическую интерпретацию производной.
Пусть кривая задана уравнением  . Угловой коэффициент касательной к ней в точке
. Угловой коэффициент касательной к ней в точке 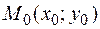 , где
, где 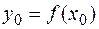 .
. 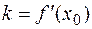 . Уравнение касательной можно найти, используя уравнение прямой, проходящей через данную точку в заданном направлении:
. Уравнение касательной можно найти, используя уравнение прямой, проходящей через данную точку в заданном направлении: 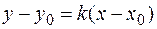 , но
, но 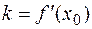 поэтому
поэтому
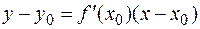
есть уравнение искомой касательной.
Так как угловые коэффициенты касательной и нормали связаны условием перпендикулярности 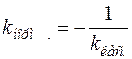 , то уравнение нормали в точке
, то уравнение нормали в точке 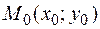 имеет вид
имеет вид
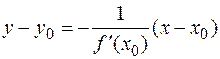 .
.
Определение. Углом между кривыми называют угол между касательными к кривым в точке их пересечения.
Определение. Две линии называют ортогональными, если они пересекаются под прямым углом.
Пример. Найти угол, под которым синусоида пересекает ось 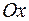 в начале координат.
в начале координат.
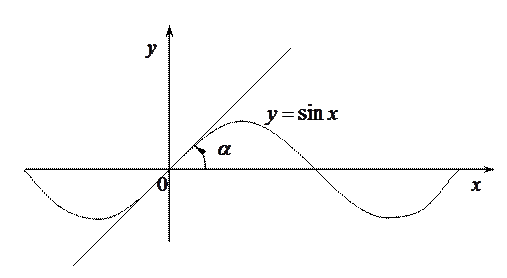
Решение. Так как 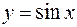 , то
, то 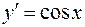
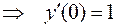 , следовательно касательная, а значит, и синусоида, пересекают ось
, следовательно касательная, а значит, и синусоида, пересекают ось 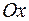 под таким углом
под таким углом 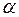 , для которого
, для которого 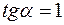 , т. е. под углом
, т. е. под углом 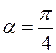 .
.
 2015-06-04
2015-06-04 13415
13415
