Дифференцируемость функции

Определение. Если для функции в точке 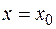существует предел

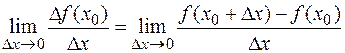, (1)

то говорят, что при данном значении 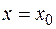функция дифференцируема

или (что равносильно этому) имеет производную.

Если функция дифференцируема в каждой точке некоторого отрезка 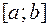(или интервала 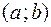), то гово­рят, что она дифференцируема на отрезке 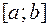(или на интервале ).

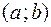Связь между непрерывностью и дифференцируемостью функции в данной точке устанавливает

Теорема. Если функция дифференцируема в некото­рой точке, то она и непрерывна в этой точке.

Доказательство. Действительно, если функция дифференцируема в точ­ке , то существует предел

,

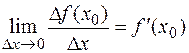Следовательно,

,

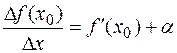где 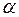― бесконечно малая функция при .

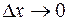Умножим последнее равенство на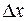

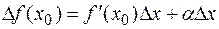(2)

Тогда

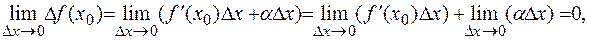
что и означает (по определению 3) непрерывность функции в точке .

⊠

Утверждение, обратное данной теореме, вообще говоря, неверно, т. е. из непрерывности функции в точке еще не следует ее дифференцируемость в этой точке.

Например, рассмотрим функцию 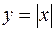. Очевидно, что эта функция определена и непрерыв­на на 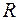. Но в точке 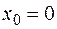не имеет производной, т.к. 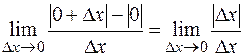не существует — не равны левосторонний и правосторонний пределы:

,

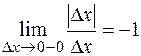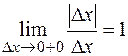
Замечание. Так как равенство (1) равносильно равенству (2), то часто функцию называют дифференцируемой в точке 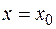, если ее приращение может быть представлено в виде (2).