Пусть 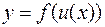 . Установим правило, позволяющее найти производную сложной функции
. Установим правило, позволяющее найти производную сложной функции 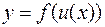 , если известны производные составляющих ее функций
, если известны производные составляющих ее функций 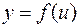 и
и 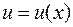 . Придадим фиксированному значению аргумента
. Придадим фиксированному значению аргумента  приращение
приращение 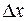 . Этому приращению соответствует приращение
. Этому приращению соответствует приращение 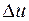 функции
функции 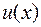 . Приращению
. Приращению 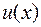 , в свою очередь, соответствует приращение
, в свою очередь, соответствует приращение 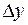 функции
функции 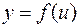 . Составим отношение
. Составим отношение
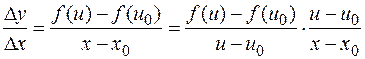 ,
,
т.е. 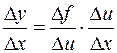 .
.
При 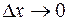 приращения
приращения 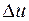 ,
, 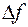 в силу дифференцируемости соответствующих функций стремятся к нулю. Так как по определению
в силу дифференцируемости соответствующих функций стремятся к нулю. Так как по определению
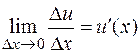 ,
, 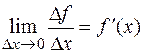 ,
,
то для функции 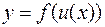
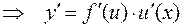 .
.
Функцию 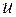 иногда называют промежуточным аргументом, а
иногда называют промежуточным аргументом, а  — основным аргументом. Таким образом, можно сформулировать следующее.
— основным аргументом. Таким образом, можно сформулировать следующее.
Правило дифференцирования сложной функции. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу и производной промежуточного аргумента по основному аргументу.
Полученное правило легко распространяется на сложную функцию, зависящую от нескольких аргументов, т. е. на композицию нескольких функций.
Пример. Найти производную функции 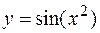 .
.
Решение. Поправилу дифференцирования сложной функции
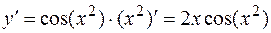 .
.
 2015-06-04
2015-06-04 527
527








