2015-06-04
1974
При раскрытии неопределенностей полезна следующая теорема, впервые доказанная И. Бернулли.
Теорема (правило Лопиталя). Если функции 
и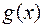 
удовлетворяют следующим условиям:
1) определены и дифференцируемы на интервале 
, причем 
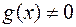и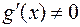 
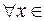
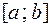, за исключением, быть может, точки 
;
2) 
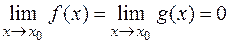(либо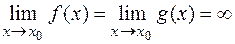 
);
3) существует предел (конечный или бесконечный) отношения производных
,
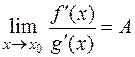то существует также предел отношения функций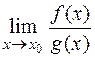 
, причем
.
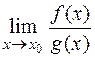
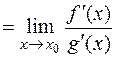Доказательство. Приведем доказательство теоремы только для случая раскрытия неопределенностей вида 
. Доопределим функции и 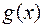в точке 
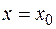, положив 
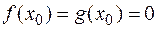. Доопределенные таким образом функции будут непрерывны в точке .
Рассмотрим отрезок |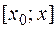 
, где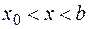 
. На этом отрезке функции и 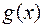непрерывны и дифференцируемы. Следовательно, по теореме Коши существует точка 
(
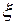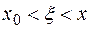) такая, что
.
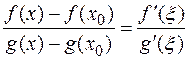Если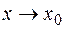 
, то и 
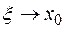, поэтому, согласно условию 3 теоремы, из последнего равенства следует, что
.
⊠
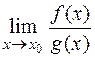
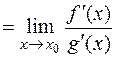Смысл правила Лопиталя заключается в том, что оно позволяет свести вычисление предела отношения функции в случае неопределенности вида или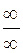 
к пределу отношения производных, который очень часто вычисляется проще.
Правило Лопиталя справедливо и в случае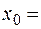 
¥.
Правило Лопиталя можно применять до тех пор, пока не будет получена дробь, для которой условия, предусмотренные теоремой, уже не выполняются.
Пример. Вычислить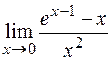 
.
Решение. Непосредственная подстановка предельного значения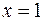 
приводит к неопределенности вида . Для ее раскрытия применим правило Лопиталя:
.
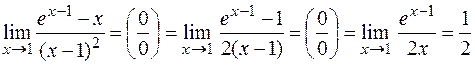Правило Лопиталя здесь применено дважды.
Замечание. Неправомерное применение правила Лопиталя, то есть если не выполняются условия теоремы может привести к неверному результату.
