Экстремум функции. Особую роль в исследовании поведения функции на множестве играют точки, разделяющие интервалы возрастания и убывания функции
Определение. Точка  называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если существует проколотая
, если существует проколотая 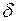 -окрестность точки
-окрестность точки  , такая, что для всех
, такая, что для всех 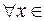
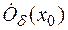 выполняется неравенство
выполняется неравенство 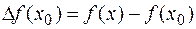 <0 (
<0 (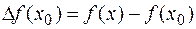 >0) Значение
>0) Значение 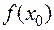 называют локальным максимумом (минимумом) функции и пишут
называют локальным максимумом (минимумом) функции и пишут
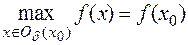 (
(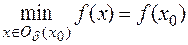 ).
).
Точки максимума или минимума функции называют точками экстремума функции, а максимумы и минимумы функции называются экстремумами функции.
Из приведенных рассуждений следует, что экстремумы функции носят локальный характер — это наибольшее или наименьшее значения функции по сравнению с близлежащими ее значениями.
Если функция  на
на 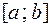 имеет несколько максимумов и минимумов, то возможен случай, когда максимум функции меньше ее минимума.
имеет несколько максимумов и минимумов, то возможен случай, когда максимум функции меньше ее минимума.
Например, на рисунке точки 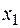 ,
, 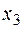 являются точками максимума функции
являются точками максимума функции  , а
, а 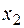 ,
, 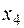 — точками ее минимума, но
— точками ее минимума, но 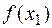 <
< 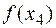 .
.
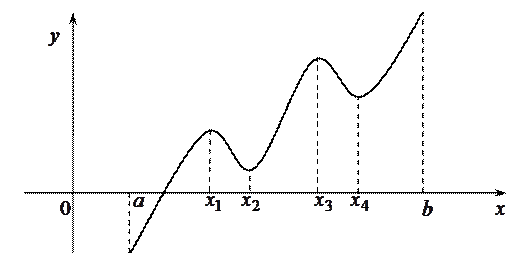
Наименьшее и наибольшее значения функции на 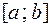 в отличие от локальных ее экстремумов называют абсолютными минимумом и максимумом функции
в отличие от локальных ее экстремумов называют абсолютными минимумом и максимумом функции  и обозначают
и обозначают 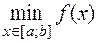 ,
, 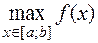
 2015-06-04
2015-06-04 502
502








