Рассмотрим случай неубывающей функции.
Необходимость: Пусть  не убывает на
не убывает на  .
.
Тогда 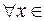
 при
при 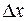 >0
>0
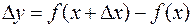 r0
r0 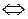
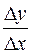 >0
>0 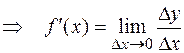 r0
r0
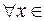
 .
.
Достаточность. Пусть  r0
r0 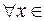
 . Тогда по формуле Лангранжа имеем
. Тогда по формуле Лангранжа имеем 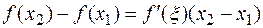 . Так как
. Так как 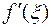 r0 (
r0 (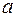 <
< 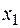 <
< 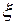 <
< 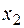 <
< 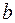 ), то
), то 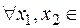
 :
: 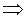
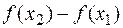 r0, т. е.
r0, т. е.  не убывает на
не убывает на  .
.
⊠
Теорема. Если же для любого 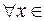

 >0 (
>0 ( <0), то функция
<0), то функция  возрастает (убывает) на этом интервале.
возрастает (убывает) на этом интервале.
Другими словами:
2)  >0
>0 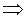
 возрастает на
возрастает на  ;
;
4)  <0
<0 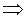
 убывает на
убывает на  .
.
Доказательство. Докажем теорему для случая возрастающей функции. Пусть  >0 на
>0 на  . Тогда для
. Тогда для 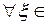

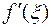 )>0 и поэтому в формуле Лагранжа, верной для
)>0 и поэтому в формуле Лагранжа, верной для 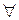
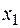 ,
, 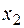
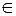

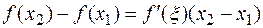 .
.
при 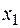 <
< 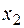
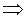
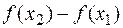 >0, т. e.
>0, т. e.  возрастает на
возрастает на  .
.
⊠
Замечание. Подчеркнем, что условия теоремы для возрастающей и убывающей функций достаточны, но не необходимы.
Например, функция 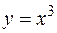 возрастает на ] — 1; 1[, однако производная в точке
возрастает на ] — 1; 1[, однако производная в точке 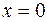 обращается в нуль.
обращается в нуль.
Геометрический смысл теоремы состоит в следующем: касательная к графику возрастающей на  функции (
функции ( > 0) составляет острый угол с положительным направлением оси
> 0) составляет острый угол с положительным направлением оси 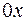 ; касательная к графику убывающей на
; касательная к графику убывающей на  функции (
функции ( <0) образует тупой угол с осью
<0) образует тупой угол с осью 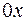 . Если функция
. Если функция  на
на  является постоянной:
является постоянной:  = C, С = const, то
= C, С = const, то  = 0 и касательная к графику функции параллельна оси
= 0 и касательная к графику функции параллельна оси 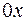 .
.
|
|
|
Пример. Найти интервалы возрастания и убывания функции 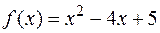 .
.
Решение. Функция 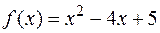 определена, непрерывна и дифференцируема на
определена, непрерывна и дифференцируема на 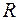 . Для отыскания интервалов монотонности функции найдем
. Для отыскания интервалов монотонности функции найдем  :
:
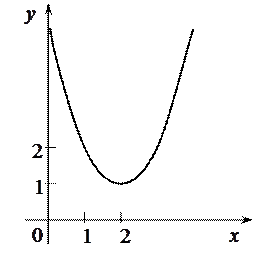
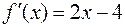 .
.
 возрастает на некотором множестве, если
возрастает на некотором множестве, если  > 0. Решим неравенство
> 0. Решим неравенство 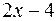 > 0. Оно выполняется при
> 0. Оно выполняется при 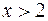 . Следовательно,
. Следовательно,  возрастает на ]2; +¥[.
возрастает на ]2; +¥[.  убывает на множестве, где
убывает на множестве, где  <0. Неравенство
<0. Неравенство 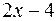 < 0 выполняется при
< 0 выполняется при 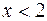 .
.
Итак, функция 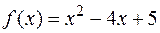 убывает на интервале ]–¥; 2[, возрастает на ]2; +¥[.
убывает на интервале ]–¥; 2[, возрастает на ]2; +¥[.
 2015-06-04
2015-06-04 580
580








