Необходимое условие существования экстремума функции

Теорема. Если в точке функция достигает экстремума, то ее производная в этой точке равна нулю или не существует.

Доказательство. Пусть в точке достигает максимума. Тогда существует 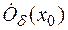, такая, что >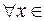

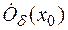
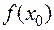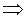
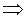
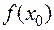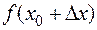> , при .

При 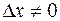>0,

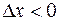
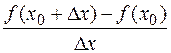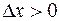
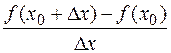При <0.

Если пределы левых частей этих неравенств при 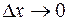сущест­вуют, то это будут соответственно производные функции справа и слева:

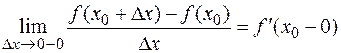r0,

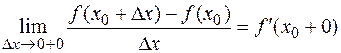b0.

Если производные функции 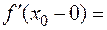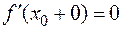в точке , то существует .

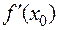
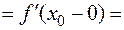
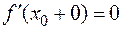Есл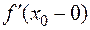и и 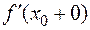отличны от нуля, то 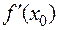не сущест­вует.

Аналогично доказывается случай, когда — точка минимума.

⊠

Геометрический смысл этой теоремы заключается в следующем: в точках экстремума функции касательная к ее графику парал­лельна оси абсцисс, если в этих точках существует производная.

Точки, в которых производная функции обращается в нуль или не существует, называют критическими или точками воз­можного экстремума. Точки, в которых производная функции обращается в нуль, называют стационарными.

Не всякая критическая точка функции является точкой ее локального экстремума. Например, производная функции 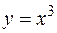в точке 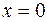обращается в ноль, но 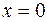не является точкой локального экстремума функции. В этой точке функция возрастает.