Не для всякой иррациональной функции можно найти первообразную, выраженную через конечное число элементарных функций. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определенных подстановок приводятся к интегралам от рациональных функций новой переменной.
Интегралы вида 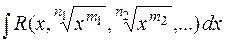 (
(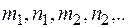 —целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от
—целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от 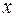 . Они вычисляются подстановкой
. Они вычисляются подстановкой 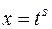 , где
, где 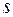 — общий знаменатель дробей
— общий знаменатель дробей 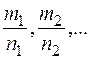 При такой замене переменной все дроби являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной
При такой замене переменной все дроби являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной 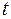 .
.
Пример. Найти 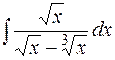 .
.
Решение. Так как общий знаменатель дробей 1/2 и 1/3 равен 6, сделаем замену 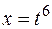 . Тогда
. Тогда
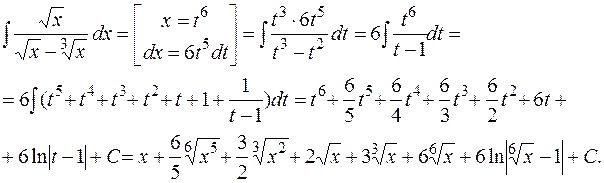
Интегралы вида 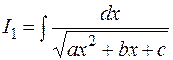 . Для нахождения таких интегралов выделяется полный квадрат под знаком радикала:
. Для нахождения таких интегралов выделяется полный квадрат под знаком радикала:
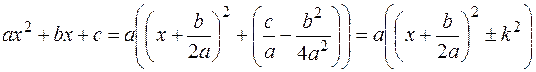
и применяется подстановка 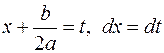 (или используется свойство №5 неопределенного интеграла
(или используется свойство №5 неопределенного интеграла 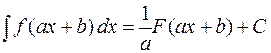 ). В результате этот интеграл сводится к табличному.
). В результате этот интеграл сводится к табличному.
Пример. Найти 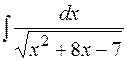 .
.
 2015-06-04
2015-06-04 1198
1198
