Интегрирование тригонометрических выражений

Рациональные функции. Условимся через 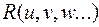обозна­чать рациональную функцию относительно 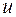, , 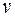,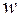..., т. е. выраже­ние, которое получено из любых величин 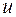, , 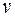,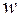..., а также действи­тельных чисел с помощью четырех арифметических действий.

Интегралы вида 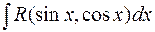. Универсальная подстановка.

Будем рассматривать интегралы вида 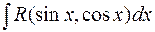при условии, что они не являются табличными. Вычислить их можно различными методами, изложенными ранее. Иногда бывает достаточно преобразовать подынтегральное выражение, ис­пользовав тригонометрические формулы, применить методы «под­ведения» множителя под знак дифференциала, замены переменной или интегрирования по частям.

Заметим, что в интегральном исчислении нет общих правил. Интегрирование может быть выполнено не единственным способом. Но даже и тогда, когда имеется теоретическое правило вычисления интеграла, оно может оказаться далеко не лучшим.

Для вычисления интегралов вида 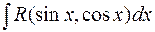существует общая уни­версальная схема вычисления, основанная на универсальной триго­нометрической подстановке 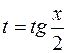. Этой подстановкой интеграл 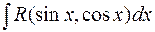преобразуется в интеграл от рациональной функции перемен­ной 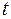, который, как было показано, всегда выражается в элементар­ных функциях.

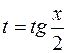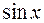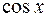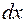Действительно, пусть . Выразим , и через :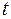

,

,

, .

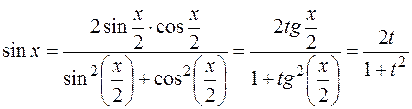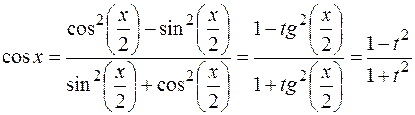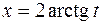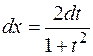Подставляя в подынтегральное выражение вместо 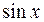, 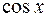и 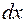их значения, выраженные через переменную 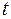, имеем

.

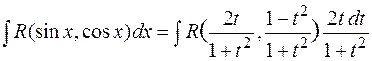Подынтегральная функция рациональна относительно 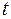. Заметим, что с помощью универсальной подстановки очень удобно вычислять интегралы вида .

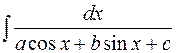Пример. Найти .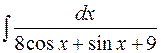

Решение. Применим универсальную подстановку :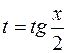

.

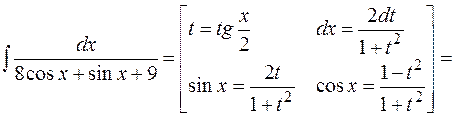
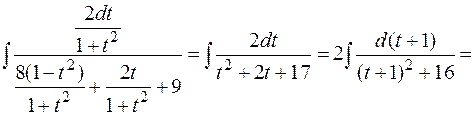
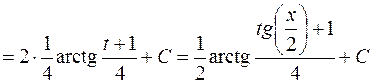Хотя универсальная подстановка всегда позволяет вычислить интегралы вида 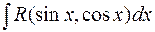, однако ее используют сравнительно редко, так как она часто приводит к интегрированию громоздких рацио­нальных дробей. Поэтому в ряде случаев более удобно использовать частные подстановки.

В частности, при вычислении интегралов вида 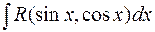можно вос­пользоваться следующими рекомендациями:

1. Если подынтегральная функция нечетна относительно 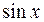, т. е. 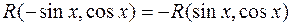, то применяется подста­новка = .

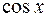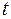2. Если подынтегральная функция нечетна относительно 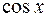, т. е. 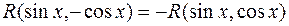, то используют подстановку = .

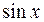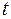3. Если подынтегральная функция четна относительно 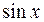и 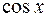, т. е. 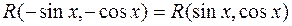, то применяется подстановка .

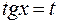Пример. Найти .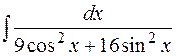

Решение. Подынтегральная функция четна относительно 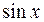и 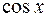. Применяем подстановку :

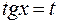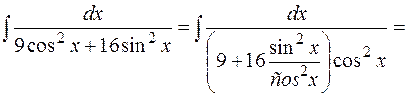
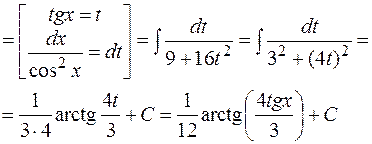
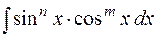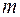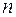
Интегралы вида (, , 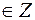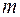r0, 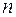r0). Если хотя бы одно из чисел 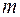или 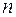— нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы 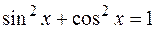оставшуюся четную степень через вторую функцию, прихо­дим к табличному интегралу.

Пример. Найти .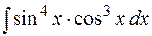

Решение.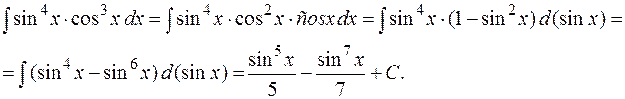

Если же 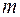и 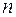— четные числа, то степени понижаются по­средством перехода к двойному аргументу с помощью тригонометри­ческих формул.