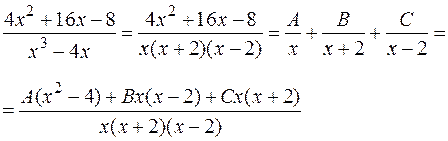
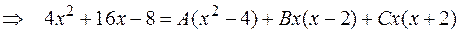 .
.
Придавая 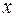 последовательно частные значения, равные корням
последовательно частные значения, равные корням 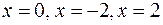 , находим:
, находим:
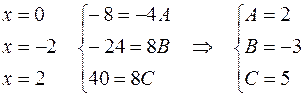
Таким образом,
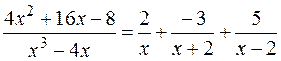 .
.
Иногда для нахождения неопределенных коэффициентов удобно применять комбинацию указанных выше методов, т. е. придавать 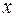 ряд частных значений и приравнивать коэффициенты при некоторых степенях
ряд частных значений и приравнивать коэффициенты при некоторых степенях 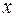 .
.
Итак, сформулируем
Правило интегрирования рациональных дробей. Для того чтобы проинтегрировать рациональную дробь, необходимо выполнить следующие действия:
1) если рассматриваемая рациональная дробь 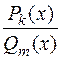 — неправильная (
— неправильная (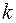 r
r 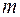 ), представить ее в виде суммы многочлена и правильной рациональной дроби:
), представить ее в виде суммы многочлена и правильной рациональной дроби:
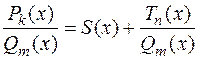
где 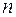 <
< 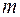 ;
; 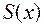 — многочлен;
— многочлен;
2) если рассматриваемая рациональная дробь 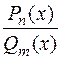 — правильная (
— правильная (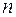 <
< 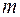 ), представить ее в виде суммы простейших рациональных дробей по формуле (1);
), представить ее в виде суммы простейших рациональных дробей по формуле (1);
3) интеграл от рациональной дроби представить в виде суммы интегралов от целой части и от соответствующих простейших дробей и вычислить эти интегралы.
Пример. Найти 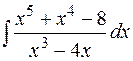 .
.
Решение. Подынтегральная дробь — неправильная, поэтому выделим сначала ее целую часть и проинтегрируем ее, а полученную правильную дробь разложим на простейшие дроби и также проинтегрируем:
|
|
|
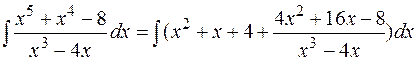
Разложение правильной рациональной дроби 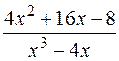 рассматривалось в предыдущем примере, поэтому запишем результат:
рассматривалось в предыдущем примере, поэтому запишем результат:
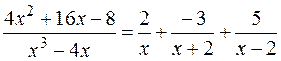 ,
,
Следовательно,
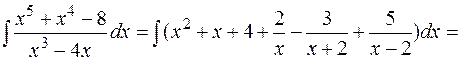
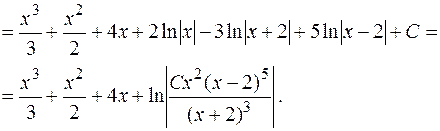
Пример. Найти 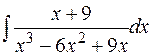 .
.
Решение. Подынтегральная функция представляет собой правильную рациональную дробь, разложим ее на простейшие дроби и проинтегрируем:
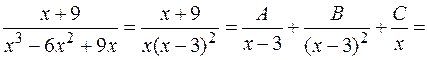
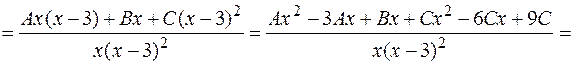
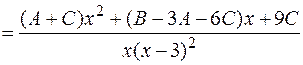
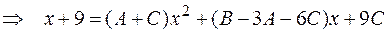 .
.
Для нахождения 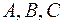 воспользуемся методом неопределенных коэффициентов, т. е. приравняем коэффициенты при одинаковых степенях
воспользуемся методом неопределенных коэффициентов, т. е. приравняем коэффициенты при одинаковых степенях 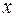 :
:
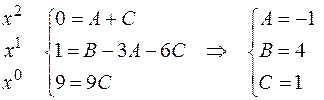 .
.
Следовательно,
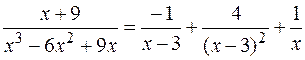 ,
,
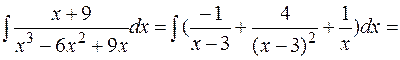
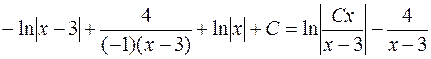 .
.
 2015-06-04
2015-06-04 708
708








