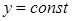Дербес туындылар

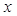деп есептеп, -ке 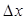өсімшесін береміз 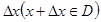. Онда 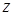функциясының 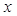бойынша дербес өсімшесі:

.

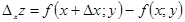Дәл осылай, 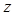функциясының 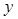бойынша дербес өсімшесін табамыз:

.

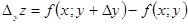Егер 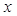пен 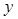-тің екеуіне де сәйкесінше 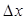, 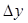өсімшелерін беретін болсақ, онда 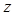функциясының толық өсімшесін аламыз:

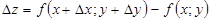(1)

Жалпы жағдайда, 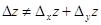болатынын айта кеткен жөн.

Анықтама 2. Егер 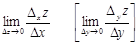табылса, оны 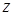функциясының 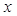бойынша [ 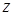функциясының 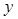бойынша] дербес туындысы деп айтамыз және былай белгілейміз:

.

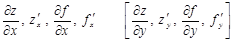2-ші анықтамадан, егер қандай да бір айнымалы бойынша дербес туынды табатын болсақ, онда бұл айнымалыдан басқа айнымалылардың барлығын тұрақты деп қарастырамыз.

Мысал 1. 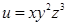функциясы берілген. Оның дербес туындылары:

.

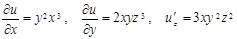1. Толық дифференциал

(1)-ші теңдіктен бірнеше түрлендірулерді жүргізе отырып, мына теңдікті аламыз:

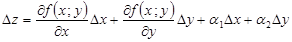, (2)

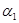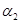
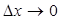мұндағы және және 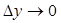шексіз кіші шамалар.

Анықтама 3. 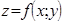функциясы (2) түрінде өрнектелсе, онда ол дифференциалданатын функция деп аталады, ал бас (сызықтық) бөлігі 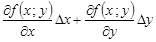толық дифференциал деп аталады және былай белгіленеді :

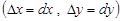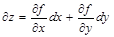
Мысал 2. 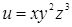функциясының 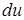толық дифференциалын тап.

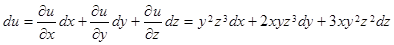
(2)-ден 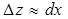екендігі шығады. Немесе

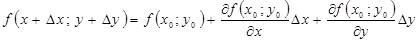
Мысал 3. 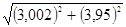жуықтап есепте.

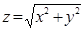функциясын қарастырамыз, мұндағы .

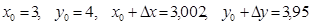Онда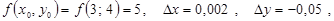

.

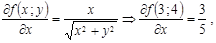
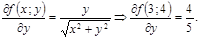
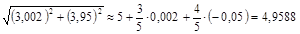3. 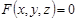айқын емес функцияның дифференциалы

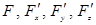табылып және үзіліссіз болса, онда

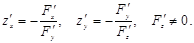
Бір айнымалы функция үшін ,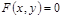

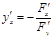
Мысал 4.

а) .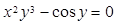

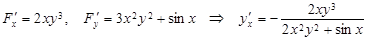
б)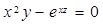

.

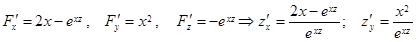4. Күрделі функцияның туындысы. Толық туынды.

функциясы берілсін, мұндағы 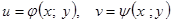. Онда 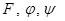функцияларының үзіліссіз дербес туындылары табылса:

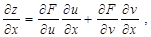
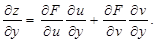
Егер 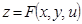функциясы берілсе, мұндағы 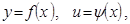онда 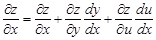- толық туындының формуласы.