Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим уравнения высших порядков, которые с помощью замены переменной сводятся к уравнениям первого порядка.

а) Дифференциальные уравнения вида y⁽ⁿ⁾ = f (x)

Найдём его общее решение.

Так как y⁽ⁿ⁾ = y^{(n - 1)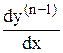}¢ = , то dy^{(n - 1)} = f (x) dx.

Интегрируя обе части, будем иметь:

y^{(n - 1)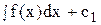} = () – это уже уравнение порядка (n – 1),

y^(n-1) = (y^{(n - 2)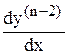})¢ = , тогда dy^{(n – 2)} = (.

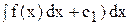Интегрируя обе части, получим:

y^{(n - 2)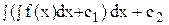} = , или

y^{(n - 2)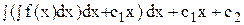} = , - уравнение порядка (n – 2).

Понижаем таким образом порядок, пока не получим y.

Пример. y^III = - ;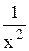

(y^II)¢ = - 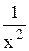; y^II = - ;

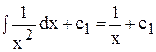(y^I)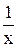^¢ = + с₁; y^I = ;

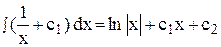y = 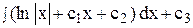, интегрируя по частям, получим:

y = 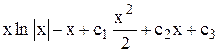- общее решение.

б) Уравнение вида: (y^II) = f (x, y')

Это уравнение не содержит явно искомой функции y.

Решение. Введём новую функцию p (x), положив y^I = p (x), тогда y^II = 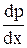= P¢. Подставляя в данное уравнение, получим: p¢ = f (x, p) – уравнение первого порядка.

Допустим, что найдено общее решение этого уравнения

p = j (x, c₁). Но так как p (x) = y^I, то y^I = j (x, c₁).

Тогда y = 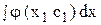+ c₂ – общее решение.

Пример. Найти частное решение данного уравнения, удовлетворяющее начальным условиям:

y^II sin x = (1 + y¢) cos x;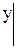

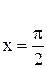
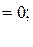
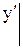
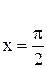
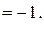
Решение. y^I= p (x), y^II = 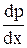. Данное уравнение примет вид:

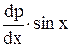= (1 + p) cos x; sin x dp = (1 + p) cos x dx.

Уравнение с разделяющимися переменными.

Делим переменные:

;

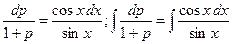ln ç1 + pç=ln çsinxç + ln çc₁ç 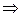1 + p = c₁ sin x;

p = c₁ sin x – 1.

Ho р = у^I, тогда

y = - c₁ cos x – x + c₂ – общее решение.

Находим частное решение, подставляя начальные условия:

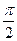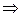1) 0 = - c₁ × - + с₂ с₂ = .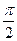

2) - 1 = c₁ – 1 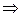c₁ = 0.

Частное решение: y = - x + .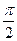

в) Уравнение вида y'' = f (y, y¢)

Оно явно не содержит аргумента x.

Решение. Для понижения порядка уравнения снова вводим новую функцию q (y), зависящую от переменной y, полагая y¢ = q (y).

Дифференцируем это равенство по x, учитывая, что y является функцией от x:

y¢¢ = 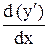= = 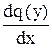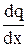× 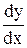, т.е. y¢¢ = q .

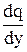Итак, y^II = qq¢. Подставляя y^I и y^II, выражaя через q, q¢, получим:

qq¢ = f (y, q) или q 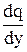= f (y, q).

Пусть функция q (y) = j (y, c₁) является общим решением этого уравнения. Учитывая, что, q (y) = 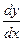получим 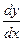= j (y, c₁) или

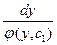= dx.

Интегрируя, получим = ,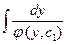

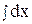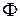(y, c₁) = x + c₂ – общий интеграл данного уравнения.

Пример. Найти общее решение уравнения 2(y^I) = (y – I)² y^II.

Решение: у' = q (y);

y'' = q q¢ = q 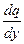; 2q² = (y – 1) q ;

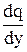1) q = 0; y¢ = 0; y = c;

2) 2q = (y – 1) ; = .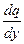

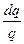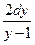Интегрируем 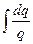: = 2 ,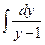

ln ï q ï = 2ln ï y - 1ï + ln ï c ₁ï Þ q = c ₁ (y – 1)²,

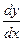= c₁ (y – 1)²; ;

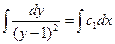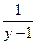– = c₁ x + c₂;

y = 1– 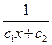- общее решение данного решения.

Итак, уравнение вида y⁽ⁿ⁾ = f (x), y¢¢ = f (x, y), y = f (x, y¢) для их решения допускают понижение порядка.

ОДНОРОДНЫЕ ЛИНЕЙНЫЕ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ