Определение. Две функции y1(x) и y2(x) называется линейно независимыми на ]a; b[, если их отношение на этом отрезке не является постоянной величиной, т.е. если 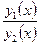 ¹ const.
¹ const.
В противном случае функции y1(x) и y2(x) называются линейно зависимыми.
Примеры 1) Функции yI(x) = ex и y2(x) = e2x будут линейно независимыми, т.к. 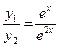 ¹ const.
¹ const.
2) Функции yI(x)=cosx; y2(x)=5cosx – линейно зависимые, т.к. 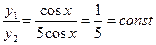 .
.
Определение. Если y1 и y2 – функции от x, то определитель
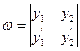 = y1
= y1 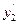 – y2y
– y2y 
называется определителем Вронского или вронскианом данных функций.
Теорема. 1. Если функции y1 и y2 – линейно зависимые функции на ]a; b[, то определитель Вронского на этом интервале тождественно равен нулю.
Действительно, если y2 = l y1, где l - const, то
y 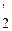 = l y
= l y  и w (y1 y2) =
и w (y1 y2) = 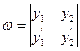 =
= 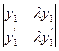 = l
= l 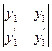 = 0
= 0
Приведём ещё одну теорему без доказательства.
Теорема.2. Если функции y1 и y2 – линейно зависимые функции на ]a; b[, то определитель Вронского w (y1 y2), составленный для этих функций, не обращается в нуль ни в одной точке указанного интервала.
Рассмотрим линейное однородное дифференциальное уравнение второго порядка:
a0 (x) yII + a1 (x)yI + a2 (x)y = 0
Так как a0 (x) ¹ 0, то, разделив обе части этого уравнения на a0, получим:
yII + 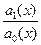 yI +
yI + 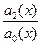 y = 0
y = 0
Обозначим 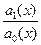 =a (x),
=a (x), 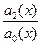 =b (x)
=b (x)
Получим: yII + a (x) yI + b (x)y = 0 (6).
Теорема (о структуре общего решения линейного однородного дифференциального уравнения второго порядка): если y1 и y2 – два линейно независимых решения уравнения (6), то
y = c1у1 + с2у2 (7),
где с1 и c2 – произвольные постоянные, есть его общее решение.
Дано: y1(x) и y2 (x) – линейно независимые решения уравнения (6), т.е
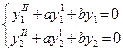 и
и 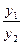 ¹ const.
¹ const.
Доказать: y = c1y1 (x) + c2y2 (x) – общее решение уравнения.
Покажем сначала, что y = c1y1 + c2y2 – решение уравнения (6). Для этого найдём yI и yII и подставим выражение y, yI, yII в уравнение (6).
y = c1y1 + c2y2
yI = c1 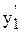 + c2y
+ c2y 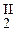
yII = c1y 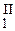 + c2y
+ c2y 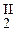
c1y 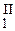 + c2y
+ c2y 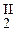 + a (c1y
+ a (c1y 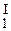 + c2y
+ c2y 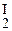 ) + b (c1y1 + c2y2) = c1(
) + b (c1y1 + c2y2) = c1(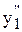 + ay
+ ay 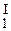 + by1) +
+ by1) +
c2 (y 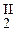 + ay
+ ay 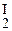 + by2) = 0, т.к. по условию теоремы y
+ by2) = 0, т.к. по условию теоремы y 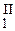 + a
+ a 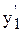 + by1 = 0 и
+ by1 = 0 и
y2II + ay 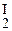 + by2 = 0.
+ by2 = 0.
Итак, y = c1y1+c2y2 – решение уравнения (6) при любых значениях c1 и c2.
Теперь докажем, что решение, y = c1y1 + c2y2 есть общее решение уравнения (6), т.е. докажем, что каковы бы ни были начальные условия
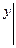
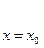
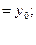 и
и 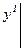
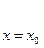
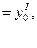
можно так подобрать значения произвольных постоянных c1 и c2, чтобы соответствующее частное решение c1y1 + c2y2 удовлетворяло заданным начальным условиям. Подставляя начальные условия в равенство (7), будем иметь:
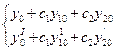 (8), где обозначено
(8), где обозначено
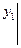
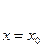 = у10,
= у10, 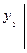
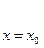
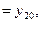
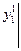
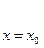
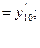 и
и 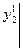
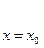
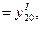
Из системы (8) можно определить c1 и c2, так как определитель системы есть определитель Вронского при x = x0 и, следовательно, не равен нулю (в силу линейной независимости y1 и y2).
Частное решение, которое получится из семейства (7) при найденных значениях c1 и c2, удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.
Доказанная теорема важна, т.к. сводит задачу нахождения общего решения уравнения (6) к более простой задаче: нахождения двух линейно независимых частных решений.
Пример. Составить общее решение уравнения yII + 2y = 0, если y1 = 1 и y2 = e-2x его частные линейные независимые решения.
Из теоремы следует, что общее решение y = c1 y1 + c2 y2.
В нашем случае: y = c11 + c2e-2x, т.е. y = c1+ c2e-2x - общее решение данного уравнения.
Пусть в уравнении (6) a(x) и b(x) - постоянные числа. Обозначим a(x)=p, b(x)=q, в этом случае и получим: yII + pyI + qy = 0 – линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами (p и q - постоянные числа).
Итак, общим решением однородного уравнения является y = c1y1 + c2y2.
 2015-06-04
2015-06-04 3986
3986
