Лекция 8
1. Промежуточный интеграл. Если мы имеем уравнение  -го порядка
-го порядка
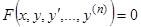 , (1)
, (1)
то, как мы уже говорили, соотношение
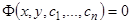 , (4)
, (4)
определяющее решение этого уравнения и связывающее 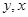 и
и  произвольных постоянных, называется общим интегралом уравнения (1). Иначе говоря, общий интеграл можно определить так: соотношение (4) называется общим интегралом уравнения (1), если, исключая из него и из уравнений, получаемых дифференцированием его по
произвольных постоянных, называется общим интегралом уравнения (1). Иначе говоря, общий интеграл можно определить так: соотношение (4) называется общим интегралом уравнения (1), если, исключая из него и из уравнений, получаемых дифференцированием его по  (причем
(причем  рассматривается как функция от
рассматривается как функция от  ) произвольные постоянные
) произвольные постоянные  , мы приходим к уравнению (1).
, мы приходим к уравнению (1).
Пусть теперь мы имеем соотношение
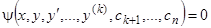 , (12)
, (12)
в которое входят производные до  -го порядка (производная
-го порядка (производная 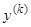 входит обязательно) и
входит обязательно) и 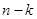 произвольных постоянных.
произвольных постоянных.
Продифференцируем это уравнение 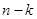 раз по
раз по  , считая
, считая  функцией
функцией  . Имеем
. Имеем
 (12.1)
(12.1)
Если в результате исключения из 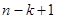 уравнений (12) и (12.1)
уравнений (12) и (12.1) 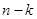 постоянных
постоянных 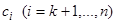 мы получим уравнение (1), то соотношение (12) называется промежуточным интегралом уравнения (1). В частности, если соотношение (12) содержит только одну произвольную постоянную, т.е. имеет вид
мы получим уравнение (1), то соотношение (12) называется промежуточным интегралом уравнения (1). В частности, если соотношение (12) содержит только одну произвольную постоянную, т.е. имеет вид 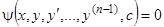 , то оно называется первым интегралом уравнения (1).
, то оно называется первым интегралом уравнения (1).
Промежуточный интеграл (12), если в нем рассматривать  как искомую функцию, сам является дифференциальным уравнением порядка
как искомую функцию, сам является дифференциальным уравнением порядка  , где
, где  . Легко видеть, что каждое решение уравнения (12) является решением уравнения (1). В самом деле, если
. Легко видеть, что каждое решение уравнения (12) является решением уравнения (1). В самом деле, если 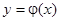 есть решение уравнения (12), то, подставляя это значение
есть решение уравнения (12), то, подставляя это значение  в уравнения (12) и (12.1), мы обратим их в тождества, а значит, и уравнение (1), которое является следствием системы (12) и (12.1), также обратится в тождество, что и требовалось доказать. Если мы найдем общее решение уравнения (12), то оно должно содержать
в уравнения (12) и (12.1), мы обратим их в тождества, а значит, и уравнение (1), которое является следствием системы (12) и (12.1), также обратится в тождество, что и требовалось доказать. Если мы найдем общее решение уравнения (12), то оно должно содержать  новых произвольных постоянных
новых произвольных постоянных 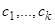 сверх входящих в само уравнение параметров
сверх входящих в само уравнение параметров 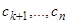 , и мы получим решение уравнения (1), содержащее
, и мы получим решение уравнения (1), содержащее  произвольных постоянных, т.е. общее решение этого последнего уравнения. Таким образом, знание промежуточного интеграла вида (12) позволяет свести задачу интегрирования уравнения
произвольных постоянных, т.е. общее решение этого последнего уравнения. Таким образом, знание промежуточного интеграла вида (12) позволяет свести задачу интегрирования уравнения  -го порядка к интегрированию уравнения порядка
-го порядка к интегрированию уравнения порядка  , т.е. к задаче, теоретически говоря, более простой.
, т.е. к задаче, теоретически говоря, более простой.
Ранее мы уже встречались с промежуточными интегралами: так, при решении уравнения (6) мы писали последовательно промежуточные интегралы с одной, двумя, и т.д. до 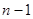 произвольными постоянными, пока не получили, наконец, общий интеграл (7). Для уравнения (9.1) мы снова находили промежуточный интеграл
произвольными постоянными, пока не получили, наконец, общий интеграл (7). Для уравнения (9.1) мы снова находили промежуточный интеграл 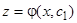 , где
, где 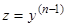 , с одной произвольной постоянной (первый интеграл). Для уравнения (10) мы имеем первый интеграл
, с одной произвольной постоянной (первый интеграл). Для уравнения (10) мы имеем первый интеграл 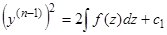 и, далее, промежуточный интеграл с двумя произвольными постоянными. И в дальнейшей нашей работе интегрирование дифференциального уравнения
и, далее, промежуточный интеграл с двумя произвольными постоянными. И в дальнейшей нашей работе интегрирование дифференциального уравнения  -го порядка будет распадаться на два шага: 1) нахождение промежуточного интеграла и 2) интегрирование уравнения, представляемого этим промежуточным интегралом.
-го порядка будет распадаться на два шага: 1) нахождение промежуточного интеграла и 2) интегрирование уравнения, представляемого этим промежуточным интегралом.
Если мы знаем два различных первых интеграла уравнения (1): 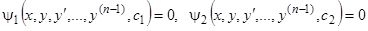 , то исключение из этих соотношений производной
, то исключение из этих соотношений производной  приведет к промежуточному интегралу, содержащему две произвольные постоянные. Аналогичный результат получим для трех, четырех, …,
приведет к промежуточному интегралу, содержащему две произвольные постоянные. Аналогичный результат получим для трех, четырех, …, 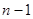 первых интегралов. Наконец, если мы знаем
первых интегралов. Наконец, если мы знаем  различных первых интегралов уравнения (1), то, исключая из них
различных первых интегралов уравнения (1), то, исключая из них 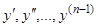 , мы придем к соотношению, связывающему
, мы придем к соотношению, связывающему 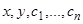 , т.е. к общему интегралу данного уравнения. Таким образом, если известны
, т.е. к общему интегралу данного уравнения. Таким образом, если известны  (различных) первых интегралов, то общее решение уравнения получается без интегрирования, при помощи исключения.
(различных) первых интегралов, то общее решение уравнения получается без интегрирования, при помощи исключения.
2. Уравнения, не содержащие явно искомой функции или независимой переменной. Пусть уравнение  -го порядка не содержит явно искомой функции
-го порядка не содержит явно искомой функции  . Для общности предположим, что оно не содержит также её
. Для общности предположим, что оно не содержит также её 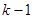 первых производных
первых производных  , и низшая производная, явно входящая в уравнение, есть
, и низшая производная, явно входящая в уравнение, есть 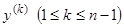 . Уравнение имеет вид
. Уравнение имеет вид
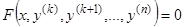 . (13)
. (13)
Полагая 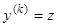 , мы заменяем уравнение (13) уравнением
, мы заменяем уравнение (13) уравнением
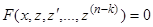 (13.1)
(13.1)
порядка 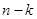 . В противоположность случаям, которые мы рассматривали ранее, здесь мы не можем утверждать, что уравнение (13.1) всегда интегрируется в квадратурах. Но вместо уравнения
. В противоположность случаям, которые мы рассматривали ранее, здесь мы не можем утверждать, что уравнение (13.1) всегда интегрируется в квадратурах. Но вместо уравнения  -го порядка мы получили уравнение порядка
-го порядка мы получили уравнение порядка 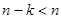 . Допустим, что мы сумели найти общий интеграл уравнения (13.1):
. Допустим, что мы сумели найти общий интеграл уравнения (13.1): 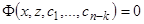 , или
, или
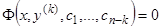 . (14)
. (14)
Уравнение (14) есть промежуточный интеграл уравнения (13), содержащий 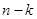 постоянных. Само уравнение (14) принадлежит к типу (6.1), т.е. заведомо интегрируется в квадратурах, и, решая его, мы найдем общий интеграл уравнения (13). Если
постоянных. Само уравнение (14) принадлежит к типу (6.1), т.е. заведомо интегрируется в квадратурах, и, решая его, мы найдем общий интеграл уравнения (13). Если  , мы непосредственно имеем уже рассмотренное нами уравнение (6.1).
, мы непосредственно имеем уже рассмотренное нами уравнение (6.1).
Пример. 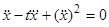 . Уравнение не содержит искомой функции и ее производной 1-го порядка. Положив
. Уравнение не содержит искомой функции и ее производной 1-го порядка. Положив 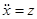 , получим
, получим 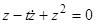 . Разделяем переменные при
. Разделяем переменные при 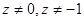 :
: 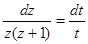 , отсюда
, отсюда  , тогда
, тогда 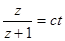 , откуда
, откуда 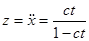 . Последовательным интегрированием получаем
. Последовательным интегрированием получаем

Рассмотрим случаи 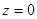 и
и  . В первом случае имеем
. В первом случае имеем 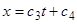 , а во втором —
, а во втором — 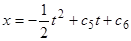 . Непосредственной проверкой убеждаемся, что эти функции также являются решениями данного уравнения.
. Непосредственной проверкой убеждаемся, что эти функции также являются решениями данного уравнения.
Пусть, далее, уравнение (1) не содержит явно  , т.е. имеет вид
, т.е. имеет вид
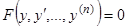 . (15)
. (15)
Здесь мы проведем такую замену переменных: в качестве новой искомой функции вводим 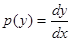 ; за независимую переменную принимаем
; за независимую переменную принимаем  . Вычисляем в этом предположении производные различных порядков:
. Вычисляем в этом предположении производные различных порядков:
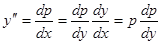 ,
,
 .
.
Таким образом, вторая производная от  по
по  выражается через
выражается через 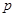 и
и  , третья производная выражается через
, третья производная выражается через 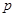 и его производные не выше второго порядка. Легко доказать методом полной индукции, что
и его производные не выше второго порядка. Легко доказать методом полной индукции, что 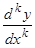 выражается через
выражается через 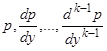 . Подставляя выражения для
. Подставляя выражения для 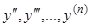 в новых переменных в уравнение (15), получим новое дифференциальное уравнение порядка
в новых переменных в уравнение (15), получим новое дифференциальное уравнение порядка 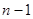 :
:  . Если его удастся проинтегрировать, то его общий интеграл
. Если его удастся проинтегрировать, то его общий интеграл  , или
, или 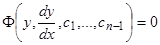 , который является промежуточным для уравнения (15), дает дифференциальное уравнение первого порядка, интегрируемое в квадратурах.
, который является промежуточным для уравнения (15), дает дифференциальное уравнение первого порядка, интегрируемое в квадратурах.
Пример. Найти решение задачи Коши
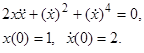
Положим  . Тогда относительно
. Тогда относительно  получим уравнение
получим уравнение 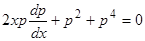 . Разделяя переменные, получим
. Разделяя переменные, получим 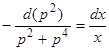 , откуда
, откуда 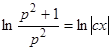 , или
, или
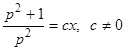 . (*)
. (*)
Постоянную  найдем, используя начальные условия. Так как
найдем, используя начальные условия. Так как 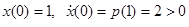 , то из (*) следует, что
, то из (*) следует, что 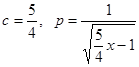 . Учитывая, что
. Учитывая, что 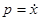 , получаем уравнение
, получаем уравнение 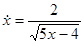 , откуда
, откуда 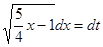 , или
, или 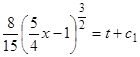 . Из условия
. Из условия 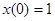 получаем
получаем 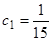 . Поэтому
. Поэтому 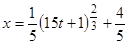 .
.
3. Понижение порядка в однородных уравнениях. Пусть левая часть уравнения (1) есть однородная функция аргументов 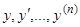 , т.е. пусть выполняется тождественно
, т.е. пусть выполняется тождественно
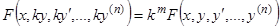 (16)
(16)
для любого  ;
; 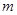 есть показатель однородности.
есть показатель однородности.
Заметим, что если 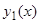 есть решение такого уравнения, то
есть решение такого уравнения, то 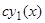 есть также решение (
есть также решение ( — произвольная постоянная). В самом деле, результат подстановки в левую часть уравнения (1) на место
— произвольная постоянная). В самом деле, результат подстановки в левую часть уравнения (1) на место  выражения
выражения 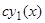 дает произведение из
дает произведение из 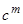 на результат подстановки в то же уравнение функции
на результат подстановки в то же уравнение функции 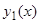 , что, по условию, тождественно равно нулю. Если мы введем новую искомую функцию
, что, по условию, тождественно равно нулю. Если мы введем новую искомую функцию 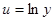 , то, по предыдущему, если
, то, по предыдущему, если  будет решением преобразованного уравнения, то
будет решением преобразованного уравнения, то 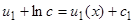 будет также его решением. Иначе говоря, уравнение допускает группу преобразований
будет также его решением. Иначе говоря, уравнение допускает группу преобразований 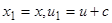 . В таком случае искомая функция
. В таком случае искомая функция 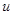 не будет входить явно в преобразованное уравнение. А тогда, как мы знаем, замена зависимой переменной
не будет входить явно в преобразованное уравнение. А тогда, как мы знаем, замена зависимой переменной 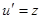 приводит к уравнению порядка
приводит к уравнению порядка 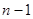 . Исключая промежуточную переменную
. Исключая промежуточную переменную 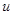 , получаем такую зависимость между
, получаем такую зависимость между  и
и 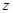 :
:
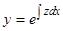 . (17)
. (17)
Итак, порядок рассматриваемого уравнения может быть понижен на единицу введением новой неизвестной функции 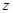 , связанной с
, связанной с  соотношением (17).
соотношением (17).
Проверим это рассуждение непосредственным вычислением. Последовательно дифференцируя равенство (17) по  , находим
, находим 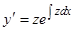 ,
, 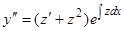 ,
,  , …, и вообще
, …, и вообще 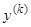 выразится как произведение
выразится как произведение 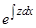 на выражение, содержащее
на выражение, содержащее 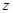 и его производные до порядка
и его производные до порядка 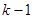 (этот факт легко доказывается полной индукцией). Вносим эти выражения в уравнение и замечаем, что в силу соотношения (16), имеем
(этот факт легко доказывается полной индукцией). Вносим эти выражения в уравнение и замечаем, что в силу соотношения (16), имеем 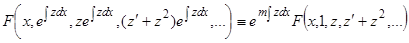 (
(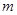 — показатель однородности). Множитель
— показатель однородности). Множитель 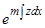 в уравнении может быть отброшен, и мы получаем уравнение порядка
в уравнении может быть отброшен, и мы получаем уравнение порядка 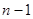 :
: 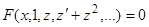 . Если его удастся решить, мы получим промежуточный интеграл уравнения (1), зависящий от
. Если его удастся решить, мы получим промежуточный интеграл уравнения (1), зависящий от 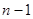 постоянных, вида
постоянных, вида 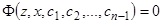 , или
, или 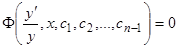 . Когда выражение функции
. Когда выражение функции 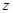 известно, то
известно, то  получится квадратурой по формуле (17), причем войдет новая постоянная
получится квадратурой по формуле (17), причем войдет новая постоянная 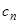 :
: 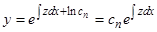 .
.
Пример. 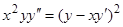 . Уравнение — однородное второй степени относительно
. Уравнение — однородное второй степени относительно 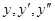 . Подстановка
. Подстановка 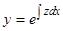 дает уравнение
дает уравнение 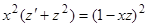 , или
, или 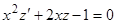 — линейное уравнение. Решаем его:
— линейное уравнение. Решаем его:  . Отсюда
. Отсюда 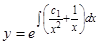 , или
, или 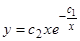 .
.
Рассмотрим этот подход в другом изложении. Итак, рассматривается уравнение  , где функция
, где функция 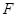 является однородной относительно
является однородной относительно 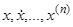 с показателем однородности
с показателем однородности 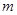 . С помощью замены
. С помощью замены 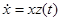 , где
, где 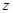 — новая неизвестная функция, порядок исходного уравнения понижается на единицу. Действительно,
— новая неизвестная функция, порядок исходного уравнения понижается на единицу. Действительно,  . Подставив эти выражения и замену
. Подставив эти выражения и замену 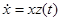 в исходное уравнение, получим
в исходное уравнение, получим  . При
. При 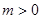 функция
функция  является решением исходного уравнения. Остальные решения получаем из уравнения
является решением исходного уравнения. Остальные решения получаем из уравнения 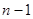 -го порядка:
-го порядка: 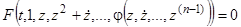 .
.
Пример. 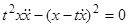 . Левая часть уравнения — однородная функция показателя 2 (см. предыдущий пример). Сделаем замену
. Левая часть уравнения — однородная функция показателя 2 (см. предыдущий пример). Сделаем замену 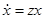 , тогда
, тогда 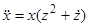 и уравнение принимает вид
и уравнение принимает вид 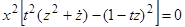 . Функция
. Функция  , очевидно, является решением данного уравнения. Остальные решения найдем из уравнения
, очевидно, является решением данного уравнения. Остальные решения найдем из уравнения 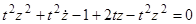 , откуда
, откуда 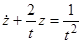 . Общее решение этого уравнения имеет вид
. Общее решение этого уравнения имеет вид  . Так как
. Так как 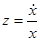 , то
, то 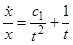 , откуда
, откуда 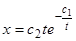 .
.
4. Уравнения, левая часть которых является точной производной. Если нам удалось убедиться, что левая часть уравнения (1) есть полная производная по  от некоторого дифференциального выражения
от некоторого дифференциального выражения 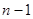 -го порядка, т.е. что мы имеем тождественно соотношение
-го порядка, т.е. что мы имеем тождественно соотношение 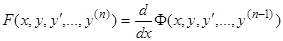 , или
, или 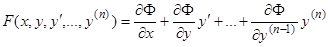 , то очевидно, что каждое решение уравнения (1) является решением дифференциального уравнения
, то очевидно, что каждое решение уравнения (1) является решением дифференциального уравнения
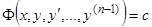 , (18)
, (18)
и обратно, каждое решение уравнения (18) является решением уравнения (1). Таким образом, соотношение (18) является первым интегралом уравнения (1); нам удалось понизить порядок уравнения на единицу.
Пример. 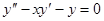 . Левая часть есть, очевидно, точная производная по
. Левая часть есть, очевидно, точная производная по  от дифференциального выражения
от дифференциального выражения 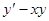 ; следовательно, имеем первый интеграл
; следовательно, имеем первый интеграл  . В данном случае легко получить в квадратурах общее решение, так как полученное уравнение — линейное первого порядка. Мы находим
. В данном случае легко получить в квадратурах общее решение, так как полученное уравнение — линейное первого порядка. Мы находим 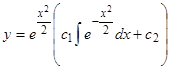 .
.
В некоторых случаях левая часть уравнения (1) не есть точная производная, но можно так преобразовать данное уравнение, чтобы в новом уравнении левая часть оказалась точной производной. Один случай применения этого метода мы видели при интегрировании уравнения (11.1), которое, при умножении на производную искомой функции, обращалось в такое уравнение, обе части которого были точными производными. Рассмотрим еще примеры.
Пример. 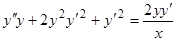 . Разделив обе части на
. Разделив обе части на 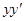 , получим
, получим  . Обе части являются точными производными. Первый интеграл имеет вид
. Обе части являются точными производными. Первый интеграл имеет вид 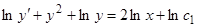 , откуда
, откуда  ; обе части опять являются точными производными. Отсюда полный интеграл
; обе части опять являются точными производными. Отсюда полный интеграл 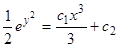 , или
, или 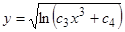 .
.
Пример. Уравнение 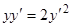 проще всего интегрируется следующим образом: делим обе части на
проще всего интегрируется следующим образом: делим обе части на 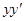 , получаем
, получаем 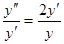 — в обеих частях стоят точные производные. Далее,
— в обеих частях стоят точные производные. Далее, 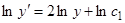 ,
, 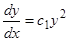 ,
, 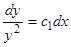 ,
,  .
.
 2014-02-02
2014-02-02 2220
2220