Занятие 3. Линейные неоднородные уравнения

1. Теорема о структуре общего решения неоднородного
дифференциального уравнения

Пусть мы имеем линейное неоднородное уравнение второго порядка

y^II + py^I + qy = f (x) - (6),

в котором коэффициенты p, q – некоторые числа, а правая часть f (x) – известная функция.

Теорема. Общее решение неоднородного уравнения (6) представляется как сумма какого–нибудь частного решения этого уравнения n и общего решения u соответствующего однородного уравнения:

y^II + py^I + qy = 0.

Доказательство.

Нужно доказать, что y = u + n (7) есть общее решение уравнения (6). Согласно условия теоремы имеем

u^II + pu^I + qu = 0; n¢¢ + pn¢ + + qn = f (x).

Подставляя y = u + n в уравнение (6), получим:

(u + n)¢¢ + p (u + n)¢ + q (u + n) = u¢¢ + n¢¢ + pu¢ + pn¢ + qu + qn =

= (u¢¢ + pu¢ + qu) + (n¢¢ + pn¢ + qn) = f (x),

так как по условию u^II + pu^I + qu = 0, n¢¢ + pn¢ + qn = f (x).

Следовательно, функция y = u + n удовлетворяет уравнению (6), т.е. является его решением.

Докажем, что y = u + n является общим решением уравнения (6). Для этого покажем, что из него можно выделить частное решение, удовлетворяющее начальным условиям:

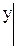
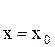
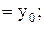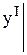
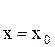
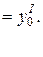и (8)

Пусть y₁(x), y₂(x) – два частных линейно независимых решения соответствующего однородного (2). Тогда

u = c₁y₁ (x) + c₂y₂ (x), где

c₁ c₂ – произвольные постоянные и

y = n (x) + c₁y₁ (x) + c₂y₂ (x). (9)

Пусть y = 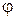(x) – какое – либо частное решение неоднородного уравнения (6), удовлетворяющее начальным условиям (8).

Покажем, что оно может быть выделено из решения (9) соответствующим подбором c₁ и c₂.

Действительно, так как

y = n (x) + c₁y₁ (x) + c₂y₂ (x) и y^I = n¢ (x) + c₁y₁ + c₂y 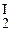(x),

то, подставляя начальные условия, получим систему уравнений для определения c₁ и c₂.

.

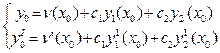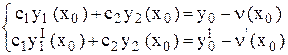. (10)

Определитель этой системы .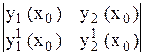

Определитель Вронского для функций y₁ и y₂ в точке x = x₀. Так как по условию y₁ (x), y₂ (x) – линейно независимые функции (решения), определитель Вронского не равен нулю и система (10) имеет единственное решение c₁₀ и c₂₀.

Полученное частное решение y = 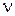(x) + c₁₀y₁ (x) + c₂₀y₂ (x) в силу теоремы единственности будет совпадать с решением y = j (x).

Таким образом, теорема доказана.

Итак, общим решением неоднородного дифференциального уравнения является y = u + n, где n - частное решение этого уравнения, а u – общее решение соответствующего однородного уравнения.