Понятие производной порядка 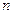 . Пусть функция
. Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности 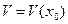 точки
точки  и дифференцируема в этой окрестности, т.е. дифференцируема в каждой точке
и дифференцируема в этой окрестности, т.е. дифференцируема в каждой точке 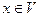 . Тогда в окрестности
. Тогда в окрестности 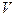 определена новая функция
определена новая функция 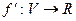 , которая, называется производной функции
, которая, называется производной функции  на множестве
на множестве 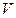 . Если функция
. Если функция 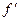 имеет в точке
имеет в точке 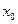 производную, то ее называют второй производной функции
производную, то ее называют второй производной функции 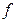 в этой точке и обозначают одним из символов
в этой точке и обозначают одним из символов
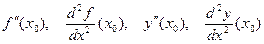
при этом часто аргумент – точку, в которой вычисляется эта производная, опускают. Таким образом.
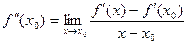 .
.
Вместе с тем, если функция 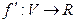 дифференцируема в точке
дифференцируема в точке 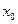 , то говорят, что функция
, то говорят, что функция 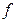 дважды дифференцируема в этой точке.
дважды дифференцируема в этой точке.
Аналогично понятию второй производной функции 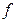 в точке
в точке 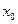 вводится понятие третьей производной
вводится понятие третьей производной 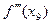 (ее обозначают также
(ее обозначают также  или
или 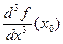 ) и, вообще производной любого порядка
) и, вообще производной любого порядка 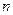 . Точнее, общее определение производной порядка
. Точнее, общее определение производной порядка 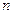 вводится индуктивно. А именно, если функция
вводится индуктивно. А именно, если функция 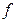 имеет в каждой точке
имеет в каждой точке 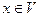 конечную производную
конечную производную 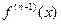 , то производная функции
, то производная функции 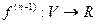 в точке
в точке 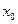 называется производной
называется производной 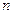 -го порядка функции
-го порядка функции 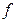 в точке
в точке 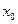 и обозначают одним из символов
и обозначают одним из символов
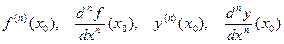 .
.
Таким образом,
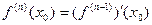
Наконец, мы будем говорить, что функция 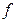
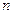 раз дифференцируема в точке
раз дифференцируема в точке 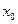 , если в некоторой окрестности этой точки она имеет конечную производную
, если в некоторой окрестности этой точки она имеет конечную производную  порядка
порядка 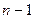 (а стало быть имеет и все производные
(а стало быть имеет и все производные 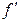 ,
, 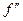 ,…,
,…, 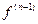 ) и функция
) и функция 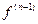 дифференцируема в точке
дифференцируема в точке 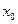 .
.
В соответствии с данным выше определением производную функции 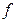 в точке
в точке 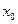 называют также первой производной функции
называют также первой производной функции 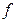 в этой точке или, также, производной первого порядка этой функции в точке
в этой точке или, также, производной первого порядка этой функции в точке 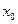 . В дальнейшем условимся считать, что
. В дальнейшем условимся считать, что
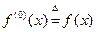 .
.
Непосредственно из определения производной 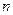 -го порядка вытекают следующие ее свойства:
-го порядка вытекают следующие ее свойства:
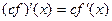 (
(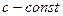 )
)
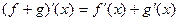 ,
,
где  и
и 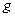 –
– 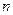 раз дифференцируемые в точке
раз дифференцируемые в точке 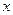 функции.
функции.
Отметим без доказательства, что если функции 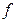 и
и 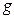 –
– 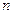 раз дифференцируемы в точке
раз дифференцируемы в точке 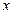 , то имеет место следующая формула (формула Лейбница):
, то имеет место следующая формула (формула Лейбница):
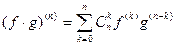
Механический смысл второй производной. Если 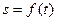 кинематический закон движения материальной точки вдоль некоторой кривой, т.е. если
кинематический закон движения материальной точки вдоль некоторой кривой, т.е. если 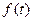 – путь, пройденный ей вдоль этой кривой к моменту времени
– путь, пройденный ей вдоль этой кривой к моменту времени 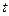 из некоторой начальной точки, то, как известно, первая производная
из некоторой начальной точки, то, как известно, первая производная 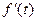 , если она существует, представляет собой мгновенную скорость точки в момент времени
, если она существует, представляет собой мгновенную скорость точки в момент времени 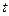 .
.
Вместе с тем отношение
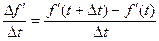
называют средним ускорением точки за отрезок времени 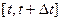 , а предел (если он существует)
, а предел (если он существует)
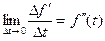
называют ускорением точки в момент времени 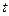 .
.
Таким образом вторая производная 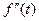 – ускорение точки в момент времени
– ускорение точки в момент времени 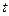 .
.
Понятие дифференциала порядка 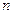 . Пусть функция
. Пусть функция 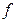
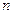 раз дифференцируема в точке
раз дифференцируема в точке 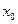 (в соответствии с данным выше определением это означает, напомним, что в некоторой окрестности этой точки она имеет конечные производные до порядка
(в соответствии с данным выше определением это означает, напомним, что в некоторой окрестности этой точки она имеет конечные производные до порядка 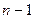 включительно, а в самой точке
включительно, а в самой точке 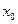 имеет и конечную производную порядка
имеет и конечную производную порядка 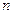 ). Тогда степенная функция
). Тогда степенная функция 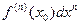 переменной
переменной 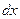 называется дифференциалом функции
называется дифференциалом функции 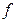 в точке
в точке 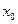 порядка
порядка 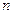 и обозначается
и обозначается  или
или 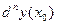 (короче также пишут
(короче также пишут 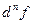 или
или  ).
).
Таким образом, для дифференциала порядка 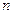 функции
функции  в точке
в точке 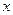 имеем формулу
имеем формулу
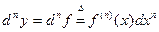 , ,
| (1) |
При этом понятия дифференциала и первого дифференциала (дифференциала порядка 1) совпадают друг с другом.
На практике вычисление дифференциалов высших порядков можно проводить по правилам, которые описываются. Предварительно условимся под арифметическим выражением понимать выражение, полученное из конечного набора функций переменной 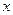 в результате следующих действий: сложения, умножения и вычисления дифференциала. Тогда вычисление дифференциалов высших порядков можно производить последовательно используя следующую формулу (при
в результате следующих действий: сложения, умножения и вычисления дифференциала. Тогда вычисление дифференциалов высших порядков можно производить последовательно используя следующую формулу (при 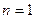 ,
, 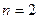 и т.д.)
и т.д.)
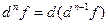 , ,
| (2) |
а также правила
1) 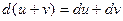 ,
,
2) 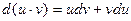 ,
,
3) 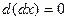 ,
,
где 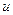 и
и 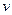 –арифметические выражения.
–арифметические выражения.
Пример 1. Найдем 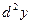 для
для 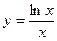 .
.
Имеем
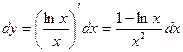 ,
, 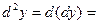 ……….
……….
 2014-02-09
2014-02-09 697
697








