Решение систем линейных уравнений с постоянными коэффициентами

Пусть мы имеем систему дифференциальных уравнений

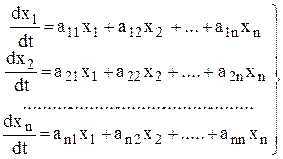, (4)

где коэффициент a_ij - постоянные величины. Здесь t – аргумент, x₁ (t), x₂ (t),…, x_n (t) – искомые функции.

Такая система называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.

Для решения системы (4) можно применять метод, с помощью которого данная система, содержащая, например три уравнения относительно трёх искомых функций, сводится к одному уравнению третьего порядка относительно одной неизвестной функции.

Этот метод называется методом исключения неизвестных.

Пример. Дана система уравнений

.

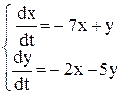Дифференцируем первое уравнение по t, находим:

= + .

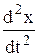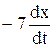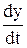Подставляя в это уравнение 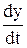из второго уравнения, получим

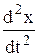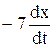= + (-2х – 5у).

Заменяя функцию у ее выражением из первого уравнения системы

y = 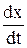+ 7х (5), приходим к линейному однородному уравнению второго порядка относительно одной функции:

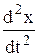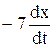= – 2х – 5( 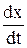+ 7х);

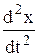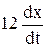+ +37х = 0;

k² + 12k + 37 = 0;

k₁,₂ = - 6 ± 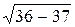= - 6 ± i;

x (t) = e^-6t ± (c₁ cost + c₂ sint).

Найдём .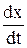

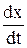= - 6 e^-6t (c₁ cost + c₂ sint) + e^-6t (-c₁ sint + c₂ cost).

Подставляя выражения для x и 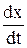в равенство (5).

y (t) = e^-6t (- 6c₁ cost - 6c₂ sint - c₁ sint + c₂ cost + 7c₁ cost + 7c₂ sint) =

= e^{- 6t} ((c₁ + c₂) cost + (c₂ - c₁) sint).

Функции х(t) = ,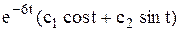

у(t) = 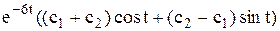являются решением данной системы.

Для выделения частного решения задаются начальные условия: х (t_o) = x_o,

у(t_o) = у_o, z(t_o) = z_o и постоянные с₁, с₂, с₃ определяются из системы уравнений

.

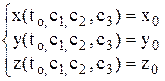Пример. Выделим из полученного общего решения

х =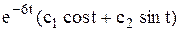

у = 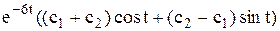частные решения удовлетворяющие начальным условиям у (0) = 1, х (0) = 0.

При заданных начальных условиях получаем систему уравнений для определения постоянных с₁ и с₂.

.

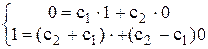с₁ = 0; с₂ = 1.

Следовательно, частное решение имеет вид:

x = 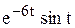; у = .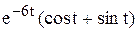

Систему (4) можно решать и другим методом, не сводя к уравнению n –го порядка. Этот метод дает возможность более наглядно анализировать характер решений.

Пусть дана нормальная система линейных дифференциальных уравнений с постоянными коэффициентами

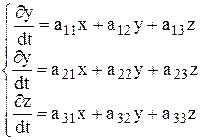. (6)

Будем искать частное решение этой системы в виде: х = aе^kt, y = bе^kt,

z = gе^kt (7).

Необходимо определить коэффициенты a, b, g и показатель степени k так, чтобы функции (7) были решением системы (6).

Найдем 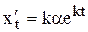, , 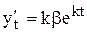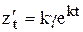и подставим в систему (6)

.

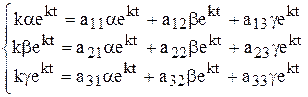Сократим на е^kt

,

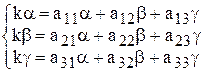перенося все члены в одну сторону получим систему линейных алгебраических уравнений относительно неизвестных a, b, g.

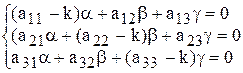. (8)

Система (8) является однородной системой уравнений. Как известно, для того чтобы однородная система имела решения, отличные от нулевого, необходимо и достаточно, чтобы определитель системы равнялся нулю.

Таким образом, для того, чтобы система (8) имела решения, отличные от нулевого, должно выполняться равенство

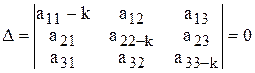. (9)

Равенство (9) представляет собой уравнение третьей степени относительно k и называется характеристическим уравнением для системы(6).

Рассмотрим случай, когда характеристическое уравнение имеет различные действительные корни k₁, k₂, k₃. Для каждого из этих корней напишем соответствующую систему уравнений (8) и определим коэффициенты a, b, g, a₁, b₁, g₁, a₂, b₂, g₂, a₃, b₃, g₃.

Если обозначить частные решения системы соответствующие корню характеристического уравнения k₁ через х₁, у₁, z₁, соответствующие корню k₂ – через х₂, у₂, z₂, и корню k₃ – через х₃, у₃, z₃, то общее решение системы дифференциальных уравнений (6) запишется в виде:

,

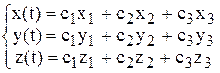или

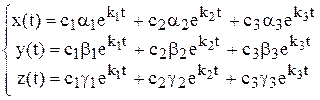. (10)

Пример. Найти общее решение системы

.

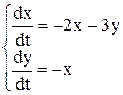Характеристическое уравнение, соответствующее данной системе имеет вид:

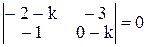или 2k + k² – 3 = 0,

k² + 2k – 3 = 0,

k₁ = – 3; k₂ = 1.

Частные решения системы будем искать в форме х₁ = a₁ 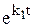, у₁ = b₁ ,

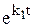х₂ = a₂ 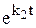, у₂ = b₂ .

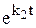Система уравнений (8) для определения a и b при k₁ = – 3 запишется в виде:

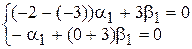или .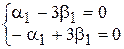

Система имеет бесконечное множество решений, так как второе уравнение есть следствие первого a₁ = 3b₁. Полагая, например, b₁ = 1, находим

a₁ = 3.

Итак, корню k₁ = –3 соответствуют частные решения х₁ = 3 ,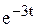

у₁ = ,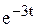

Система уравнений (8) для определения a и b при k₂ = 1 записывается в виде:

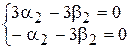
откуда a₂ + b₂ = 0, или a₂ = – b₂.

В качестве решения системы можно взять a₂ = 1, b₂ = –1. Тогда корню
k₂ = 1 соответствуют частные решения х₂ = е^t и у₂ = –е^t.

Общее решение данной системы согласно формуле (10):

.

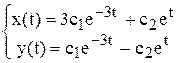Таким образом, решать систему линейных уравнений можно несколькими способами.