Доказательство

Так как f (x) интегрируема на [a; b], то существует конечный предел n-ой интегральной суммы, который не зависит ни от способа разбиения области интегрирования на части, ни от выбора точек С_i внутри частичных областей. Это позволяет при составлении каждой интегральной суммы включить точку c в число точек разбиения. Пусть с = х_к. Тогда интегральная сумма будет состоять из двух частей, одна из которых относится к [a; с], другая к [с; b]:

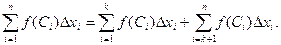
Переходя к пределу при l ® 0, имеем:

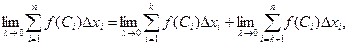
или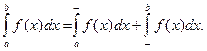

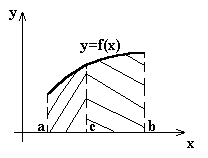
Геометрически: площадь криволинейной трапеции с основанием [a; b] равна сумме площадей криволинейных трапеций с основаниями [a; с] и [с; b]

Замечание. Нетрудно убедиться, что выведенная формула будет справедлива и для случая, когда точка с лежит вне отрезка [a; b].

4. Свойство неотрицательности определенного интеграла.

Если на отрезке [a; b] f (x) ³ 0, то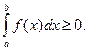

Действительно, т.к. f (C_i) ³ 0 и Dx_i > 0, то 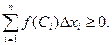Поэтому и предел интегральной суммы при l ® 0, т.е.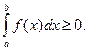

5. Интегрирование неравенств. Если на отрезке [a; b], две функции f (x) и j (х) удовлетворяют неравенству: f (x) ³ j(x), то .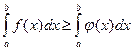

Другими словами, неравенство можно почленно интегрировать.

У нас разность f (x) - j (x) 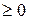. По свойству (4) 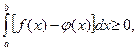но

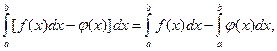откуда .

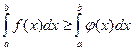6. Если а = b, то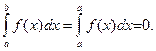

7. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

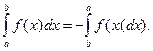
8. Если функция f(x) = 1 на отрезке [a; b], то интеграл от -нее дает длину этого отрезка: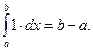

9. Ограниченность определенного интеграла.

Пусть значения функции в любой точке отрезка [a; b] не больше числа М и не меньше числа m: m £ f (x) £ M.

Тогда m (b - a) £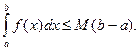

Доказательство. Если m £ f(x) £ M, то по свойствам 5, 1 и 8 получим:

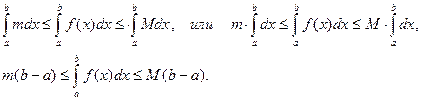
10. Теорема о среднем.

Если f (x) непрерывна на отрезке [a; b], то существует такая точка c внутри этого отрезка, что:

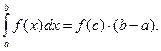
Доказательство. Обозначим через m и M соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a; b]. Тогда m £ f(x) £ M, " xÎ [a; b].

По свойству (9) (геометрически оно означает, что площадь заштрихованной части является промежуточным значением между площадями двух прямоугольников с общим основанием (b - a) и высотами M и m):

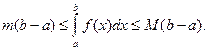
Разделив это неравенство на (b - a), получим:

m £ 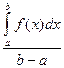£ M. Обозначим 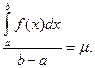Тогда m £ m £ M, т.о. m является промежуточным числом между наименьшим значением m функции f(x) и ее наибольшим значением М, следовательно, найдется такое значение с Î (a; b), для которого f(c) = m или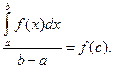

Отсюда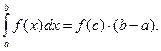

Значение функции f (x) в точке х = с называется средним значением функции на отрезке [a; b].

Итак, свойства определённого интеграла мы будем использовать при его вычислении.