Несобственные интегралы

1. Несобственные интегралы с бесконечными пределами

Вспомним определение интеграла 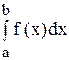как предела интегральных сумм: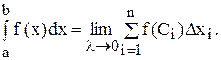

В определении предполагается, что интервал интегрирования конечен, а функция f (x) непрерывна в нем. Нарушение этих предположений приводит к несобственным интегралам.

Определение. Если интеграл 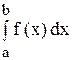стремится к конечному пределу при неограниченном возрастании “b”, то этот предел называют несобственным интегралом с бесконечной верхней границей от функции f (x) и обозначают символом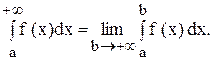

В этом случае говорят, что несобственный интеграл 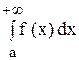существует или сходится.

Если указанный предел не существует или существует, но бесконечен, то говорят, что интеграл не существует или расходится.

Аналогично определяется несобственный интеграл с бесконечной нижней границей:

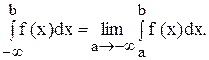
Несобственный интеграл с двумя бесконечными границами определяется формулой:

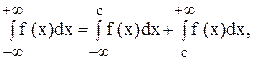
где с - любая фиксированная точка на оси Ох.

Итак, несобственные интегралы могут быть с бесконечно нижней границей, с бесконечно верхней границей, а также с двумя бесконечными границами.

Признаки сходимости. Абсолютная и условная сходимость

Интеграл 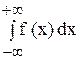существует только тогда, когда существует каждый из интегралов: 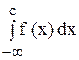и .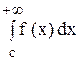

Пример. Исследовать на сходимость интеграл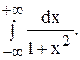

Полагая с = 0, получим:

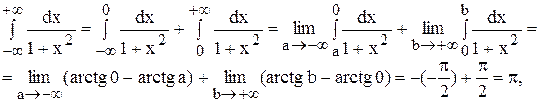
т.е. интеграл сходится.

Иногда нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится, сравнив его с другим интегралом.

Теорема сравнения несобственных интегралов.

Пусть в интервале [a; +¥) функции f (x) и j (х) непрерывны и удовлетворяют неравенству 0 £ j (x) £ f (x). Тогда:

а) если интеграл 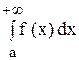сходится, то сходится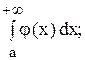

б) если интеграл 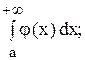расходится, то 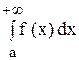также расходится.

Пример.1. Исследовать, сходится ли интеграл:

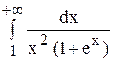
Решение. Заметим, что при 1 £ x:

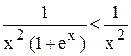
Далее,

= 1

Следовательно, 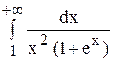сходится и его значение, меньше 1.

Пример. 2. Исследовать, сходится ли интеграл

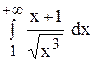
Замечаем, что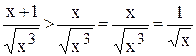

Но, .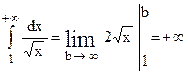

Следовательно, расходится и данный интервал.

Теорема. Если интеграл 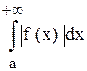сходится, то сходится и интеграл .

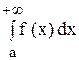В этом случае последний интеграл называется абсолютно сходящимся.

Если интеграл от 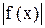расходится, то об интеграле от f (x) на одном этом основании ещё ничего сказать нельзя: он может расходиться, а может и сходиться. В последнем случае (т.е. когда 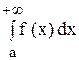сходится, 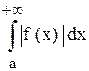расходится говорят, что 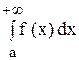сходится условно (не абсолютно).

Пример. Исследовать сходимость интеграла

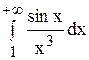
Здесь подынтегральная функция – знакопеременная.

Замечаем, что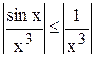

Но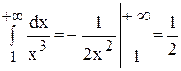

Следовательно, интеграл 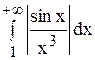сходится.

Отсюда следует, что сходится и данный интеграл.

Итак, для определения сходимости несобственного интеграла можно его сравнивать с другим интегралом, который заведомо сходится или расходится.

Несобственные интегралы от разрывных функций

Если на отрезке [a; b] функция f (x) имеет несколько (конечное число) точек разрыва первого рода, это “препятствие” легко устранить, разбив отрезок точками разрыва на несколько отрезков, вычислить определенные интегралы на каждом отдельном участке и результаты сложить.

Рассмотрим определенный интеграл от функции, неограниченной при приближении к одному из концов отрезка [a; b], например, .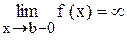

(В таких случаях обычно говорят: ’’Функция имеет бесконечный разрыв на правом конце отрезка интегрирования’’.)

Ясно, что обычное определение интеграла здесь теряет свой смысл.

Определение. Несобственным интегралом от функции f(x), непрерывной при а £ х < b и неограниченной при x ® b - 0, называется предел:

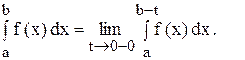
Аналогично определяется несобственный интеграл от функции, имеющей бесконечный разрыв на левом конце отрезка:

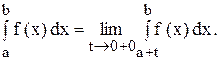
Если точка с бесконечного разрыва находится внутри интервала (a; b), то:

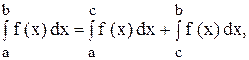
причем исходный интеграл называется сходящимся, если существуют оба интеграла в правой части этого равенства, причем независимо друг от друга.

Пример 1. Вычислить интеграл: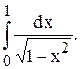

Подынтегральная функция стремится к ¥ при х ® 1, поэтому:

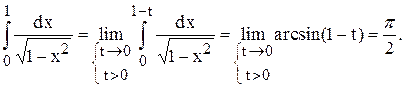
Пример. 2. Вычислить интеграл .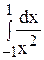

Так как внутри отрезка интегрирования существует точка x = 0, где подынтегральная функция разрывна, то и интеграл нужно представить как сумму двух слагаемых:

.

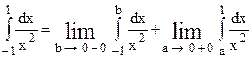Вычислим каждый предел отдельно:

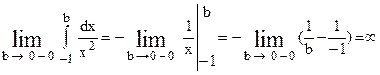
Следовательно, на участке [ -1, 0] интеграл расходится.

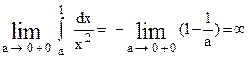
Значит на участке [0, 1)] интеграл также расходится.

Таким образом, данный интеграл расходится на всем отрезке [-1, 1]. Отметим, что если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке x = 0, то получили бы неверный результат. Действительно,

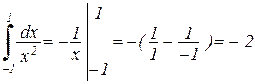, что невозможно.

Итак, для исследования несобственного интеграла от разрывной функции, необходимо "разбить" его на несколько интегралов и исследовать их.