Занятие 2. Методы интегрирования

1. Производная интеграла по переменному верхнему пределу

Непосредственное вычисление интегралов, как пределов интегральных сумм, чрезвычайно громоздко и на практике применяется крайне редко. Основной формулой для вычисления определенных интегралов служит формула Ньютона-Лейбница, которая будет получена в дальнейшем.

Пусть на отрезке [a; b] задана непрерывная функция f (x). Будем рассматривать определенный интеграл с переменным верхним пределом х,

где xÎ[a; b]: .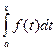

Ясно, что этот интеграл является функцией от своего верхнего предела, при изменении которого будем получать различные значения интеграла.

Значение данной функции изображается площадью криволинейной трапеции, приходящейся на отрезок [a; x]. Обозначим эту функцию Ф(х):

.

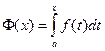Найдем ее производную.

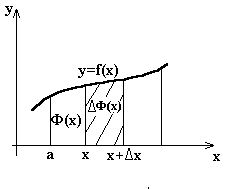Дадим х приращение Dх (x+DxÎ[a; b]), тогда:

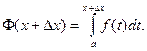
Приращение DФ функции Ф(х) будет:

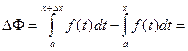S_заштр. =

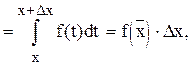где 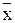- промежуточное значение между 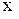и .

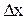Составим отношение 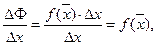тогда:

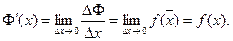
Итак, Ф’(x) = f (x).

Теорема Барроу. Производная интеграла с переменным верхним пределом по этому верхнему пределу равна значению подынтегральной функции на верхнем пределе интегрирования:

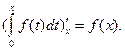
Следствие. Интеграл 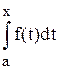с переменным верхним пределом интегрирования есть первообразная для подынтегральной функции f (x). В частности, отсюда вытекает, что любая непрерывная функция имеет первообразную.

Итак производную интеграла по переменному верхнему пределу будем применять в дальнейшем при рассмотрении нашего следующего вопроса.

2. Формула Ньютона-Лейбница

Мы установили, что функция 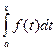является первообразной для непрерывной функции f (x). Обозначим через .

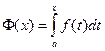Пусть F (x) - произвольная первообразная для f (x) на отрезке [a; b]. По свойству первообразных:

Ф(х) – F (x) = c = const.

Поэтому 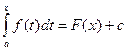для любых xÎ[a; b].

Определим константу с.

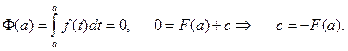
Итак,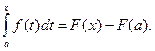

Положив х = b, будем иметь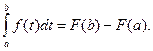

Так как переменная интегрирования может быть заменена любой другой буквой, то, положив t = x, получим окончательно:

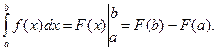
Полученная формула носит название формулы Ньютона-Лейбница и читается так: чтобы вычислить значение интеграла, надо взять любую первообразную f (x) для интегрируемой функции f (x) и составить разность ее значений, вычисленных при верхнем и нижнем пределах интегрирования.

Примеры: 1.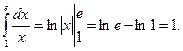

2.

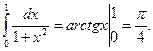
3.

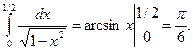
Для разрывных функций формула Ньютона-Лейбница может и не иметь места.

Таким образом, формула Ньютона – Лейбница применяется для вычисления определённого интеграла.

3. Замена переменной в определенном интеграле

Часто применяемым приемом для вычисления определенного интеграла является, как и в случае неопределенных интегралов, замена переменной (подстановка).

Пусть дан 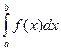от функции f(x), непрерывной на отрезке [a; b]. Заменим: х = j (t), a £ t£ b.

Если:

1) функция х = j (t) непрерывна вместе с j¢(t) на отрезке [a; b];

2) при изменении t от a до b значения функции х = j (t) не выходят за пределы отрезка [a; b];

3) j (a) = a, j(b) = b,

то: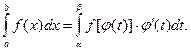

Докажем это. Пусть F(x) - первообразная для f(x), т.е. F¢(x) = f(x).

Тогда по формуле Ньютона-Лейбница:

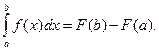
Если в первообразной F(x) положить х = j (t), то F[j (t)] будет первообразной для f [j(t)] j¢(t), т.к.:

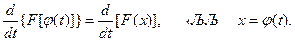
По правилу дифференцирования сложной функции имеем:

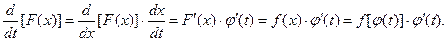
Поэтому по формуле Ньютона-Лейбница получим:

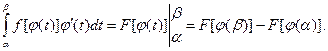
Учитывая условия 3: j(b) = b, j(a) = a, получим

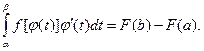
Замечание. Напоминаем, что возвращаться к старой переменной при подстановке не нужно, а переменная t должна однозначно выражаться через х.

Пример.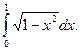

Пусть x = sint, при х= 0, t = 0; при х = 1, t = .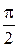

Функция x = sint и ее производная на отрезке [0; 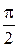] непрерывны. При изменении t от 0 до 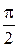значения функции x = sint не выходят за пределы отрезка [0; 1]. Тогда:

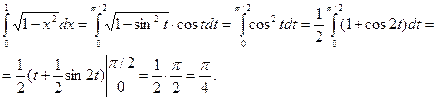
При использовании формулы замены переменной в определенном интеграле необходимо проверять выполнение перечисленных выше условий. Если эти условия нарушаются, замена переменной может привести к абсурду:

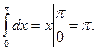
С другой стороны,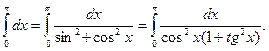

Формальная подстановка tgx = t приводит к следующему результату:

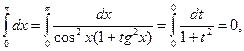т.е. p = 0.

Итак, простейшим способом вычисления определённого интеграла есть метод замены переменной, который можно использовать при выполнении трех условий, которые мы рассмотрели.

4. Интегрирование по частям в определённом интеграле

Пусть u = u (x) и v = v (x) - две функции, непрерывные вместе со своими производными на отрезке [a; b]. Имеет место формула интегрирования по частям:

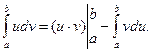
Вывод ее немедленно следует из формулы интегрирования по частям для неопределенного интеграла. Действительно,

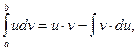поэтому:

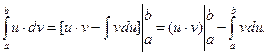
Пример

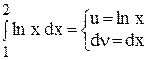
1) 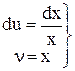= (x ln x) – 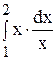= 2 ln2 – ln1 – 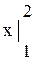= = 2 ln2 – 1;

2) 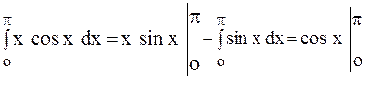= – 1 – 1 = – 2

Итак, для решения определённых интегралов сложных функций применяется метод интегрирования по частям.