Средние показатели динамического ряда

К средним показателям динамического ряда относятся:

- средний уровень ряда;

- средний абсолютный прирост;

- средний темп роста;

- средний темп прироста.

Для периодического ряда средний уровень ряда находится по средней арифметической простой:

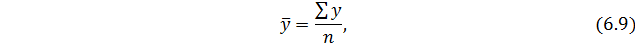
где 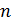- число уровней ряда динамики.

Если анализируется моментный ряд, то для определения среднего уровня ряда используется средняя хронологическая:

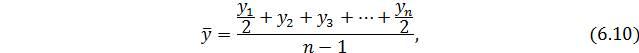
Пример 1. Численность работников предприятия связи на начало каждого квартала составила:

на 1 января 202 чел.;

на 1 апреля 208 чел.;

на 1 июля 209 чел.;

на 1 октября 212 чел.;

на 1 января следующего года 218 чел.

Среднегодовая численность работников составила:

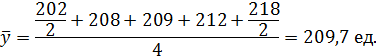
Средняя хронологическая используется, если уровни ряда равно отдалены друг от друга.

Если моментный ряд динамики имеет неодинаковые промежутки времени между датами, то используется средняя арифметическая взвешенная:

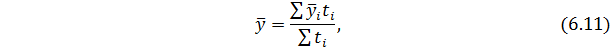
где 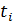- период времени между соседними уровнями;

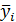- среднее значение между соседними уровнями.

Пример 2. Стоимость основных производственных фондов составила:

на 1 января 12800 тыс. руб.,

на 1 марта 13100 тыс. руб.,

на 1 сентября 15200 тыс. руб.,

на начало следующего года 15300 тыс. руб.

Среднегодовая стоимость основных фондов будет равна:

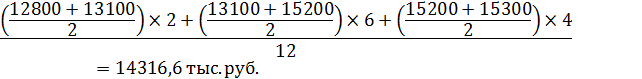
Средний абсолютный прирост:

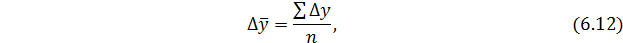
где n – количество абсолютных приростов.

Средний темп роста:

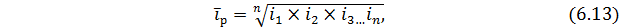
где 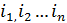– темпы роста цепные;

n – количество темпов роста.

Средний темп прироста рассчитывается:

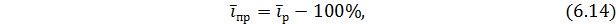
Динамические ряды графически изображаются в виде столбиковых или линейных диаграмм.

Пример 3. В таблице представлены данные о доходах предприятия связи за 5 лет. Проанализировать ряд динамики, рассчитав при этом соответствующие показатели.

Таблица 6.1

Годы
Доходы, в млн. руб.

Для удобства все расчеты сводятся в аналитическую таблицу следующего вида:

Таблица 6.2 Расчетная таблица

Абсолютный прирост, млн. руб.	цепной	-
базисный	-
Темп роста, %	цепной	-	104,8	115,3	101,3	103,1
базисный	-	104,8	120,9	122,5	126,4
Темп прироста, %	цепной	-	4,8	15,3	1,3	3,1
базисный	-	4,8	20,9	22,5	26,4

Рассчитывается средняя сумма доходов за 5 лет:

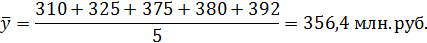
Средний абсолютный прирост будет равен:

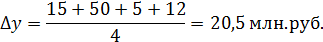
Определяется средний темп роста доходов:

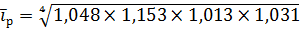=1,12 или 112%.

Средний темп прироста составит:

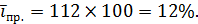
Динамический ряд изображается в виде линейной диаграммы:

Доходы, млн. руб.

t

y

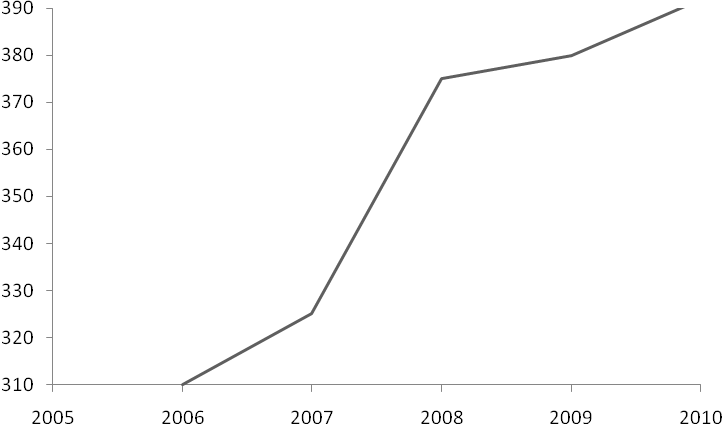
Рис. 6.1. Динамика доходов предприятия

Ряд имеет тенденцию роста. Доходы предприятия увеличиваются ежегодно, в на 20,5 млн. руб. или на 12%. Наибольший рост доходов получен в 2008 г. по сравнению с 2007 г., а наименьший рост наблюдался в 2009 г. по сравнению с 2008 г.