2015-06-05
1019
Для выявления общей тенденции изменения показателей динамического ряда используется выравнивание динамического ряда, которое является одним из приемов обработки динамического ряда. Выравнивание осуществляется разными способами:
- укрупнение периодов ряда;
- аналитическое выравнивание.
Способ укрупнения периодов ряда представляет собой замену фактических уровней ряда теоретическими уровнями, которые относятся к более продолжительным периодом времени.
Пример 4. Обмен по денежным переводам в почтамте по месяцам года:
Таблица 6.3
| Месяцы | январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| Денежные переводы, тыс. ед. |
Из таблицы видно, что ряд имеет колеблемость и без предварительной обработки этого ряда трудно ответить на вопрос, какую тенденцию имеют уровни ряда.
По методу укрупнения периодов ряда данные о денежных переводах представляются поквартально:
I квартал – 70 тыс. ед.;
II квартал – 72 тыс. ед.;
III квартал - 75 тыс. ед.;
IV квартал – 82 тыс. ед.
Данный способ позволил выявить, что анализируемый ряд имеет тенденцию роста.
Метод скользящей средней заключается в том, что фактически уровни ряда заменяются теоретическими, которые рассчитываются, используя средние величины из уровней ряда. Обычно средние рассчитываются по трем уравнениям (n =3). Однако если по полученным средним тенденция не обнаруживается, то количество уровней берется 5 (n =5).
Для предыдущего примера при n =3, теоретические уровни ряда будут определяться следующим образом:
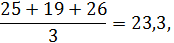
это значение будет относиться к февралю;
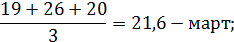
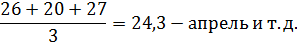
Полученный теоретический ряд представлен в таблице 6.4.
Таблица 6.4
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| Денежные переводы, тыс. ед. | - | 23,3 | 21,6 | 24,3 | 24,3 | 24,6 | - |
Ряд имеет тенденцию роста. Эмпирические и выровненные ряды представлены на рис. 6.2.
| y |
| фактическая линия |
| теоретическая линия |
| t |
Рис. 6.2. Эмпирический и выровненные ряды
Аналитическое выравнивание – наиболее распространенный метод обработки динамического ряда, он позволяет не только анализировать динамический ряд, но и осуществлять прогнозы на последующие периоды.
Сущность данного метода состоит в том, что фактические уровни заменяются теоретическими, которые плавно изменяются согласно прямой или кривой линии.
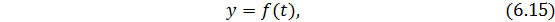
Чаще всего в качестве выравнивающей функции применяется уравнение прямой линии:
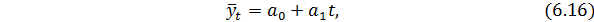
где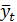 
- выравненные уровни;
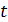- номера по порядку периодов времени;
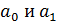- параметры уравнения прямой линии.
Для нахождения параметров 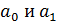используется метод наименьших квадратов, при этом решается система уравнений:
| (6.17) |
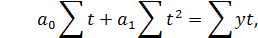
где n –количество уровней динамического ряда.
Для упрощения решения принимается, что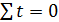 
и тогда система уравнений принимает следующий вид:
| (6.18) |
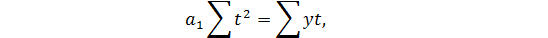
Из этой системы находится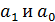 
:
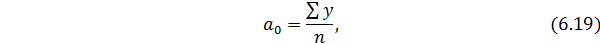
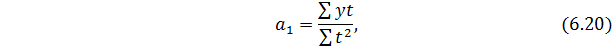
Чтобы найти теоретические (выравненные) значения уровней ряда необходимо в уравнение прямой подставить вместо t условные обозначения периодов времени.
Пример 5. В таблице 6.5 приведены данные о товарообороте по месяцам года. Выявить тенденцию динамического ряда методом аналитического выравнивания.
Таблица 6.5
| Месяцы | январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| Товарооборот фирмы, млн. руб. |
Для выполнения расчетов составляется расчетная таблица 6.6.
Таблица 6.6 Расчетная таблица
| Месяцы | Товарооборот фирмы, млн. руб., y | Условные обозначения периода, t |  |  |  |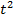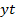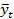
| Январь | -11 | -1121 | 100,15 | ||
| Февраль | -9 | -949 | 101,85 | ||
| Март | -7 | -728 | 103,5 | ||
| Апрель | -5 | -530 | 105,25 | ||
| Май | -3 | -306 | 106,95 | ||
| Июнь | -1 | -113 | 108,65 | ||
| Июль | +1 | +95 | 110,35 | ||
| Август | +3 | +354 | 112,05 | ||
| Сентябрь | +5 | +560 | 113,75 | ||
| Октябрь | +7 | +854 | 115,45 | ||
| Ноябрь | +9 | +1008 | 117,15 | ||
| Декабрь | +11 | +1364 | 118,85 | ||
| ИТОГО |
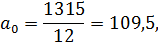
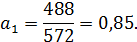
Уравнение принимает следующий вид:
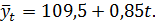
Подставляя вместо t поочередно (-11, -9, -7 и т.д.), получаем выравненные (теоретические) значения динамического ряда.
Обобщая полученные данные можно сделать вывод, что ряд имеет тенденцию роста, ежемесячно товарооборот фирмы в среднем возрастает на 1,7 млн. руб.
Эмпирические и теоретические уровни ряда представлены на рис. 6.3.
| Товарооборот фирмы (млн. руб.) |
| Месяцы, годы |
 |
фактическая линия
теоретическая линия
| Рис. 6.3. Фактический и выравненный ряды динамики товарооборота фирмы |
