Интерполяция – это метод определения значений промежуточных уровней ряда, которые по каким-либо причинам оказались неизвестными.
Существует несколько способов интерполяции:
1. Неизвестное значение уровня ряда находится как среднее арифметическое из соседних уровней ряда:
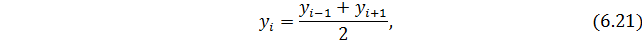
2. Промежуточное значение уровня ряда, которое неизвестно, можно определить по абсолютному приросту из соседних уровней:
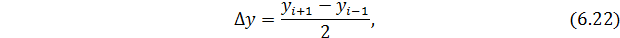
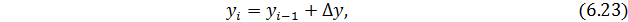
3. Следующий способ интерполяции основывается на определении среднегодового темпа роста:
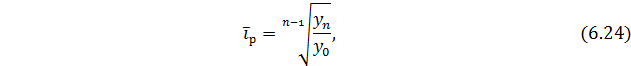
где 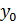 – начальный уровень ряда;
– начальный уровень ряда;
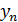 - конечный уровень ряда;
- конечный уровень ряда;
n – число уровней ряда.
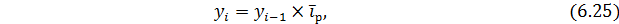
Пример 6. В таблице 6.7 приведены данные об объеме продукции предприятия за 5 лет, причем отсутствуют данные за 2008 г. Необходимо найти недостающий уровень всеми способами.
Таблица 6.7
| Годы | |||||
| Объем продукции, тыс. руб. | ? |
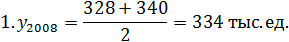
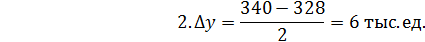
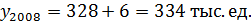
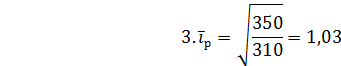
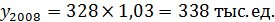
Экстраполяция – метод определения количественных характеристик для совокупностей и явлений, которые не подвергались наблюдению. Экстраполяция используется при прогнозировании.
Прогнозирование – это оценка будущего на основе глубокого анализа тенденций развития социально-экономических явлений и их взаимосвязей, в прошлом.
Существует несколько способов прогнозирования:
1. Прогнозированное значение можно определить с использованием среднего абсолютного прироста:
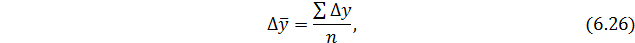
где 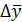 - средний абсолютный прирост;
- средний абсолютный прирост;
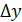 - абсолютные приросты по годам;
- абсолютные приросты по годам;
n –количество приростов.
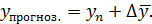
Используя данные предыдущего примера 6, выполняется прогноз на 2010 г.:
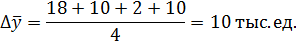
Для 2008 г. уровень ряда взят 338 тыс. ед.:
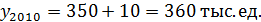
Данный способ применяется в том случае, если развитие явления происходит по арифметической прогрессии.
2. Следующий способ прогнозирования основывается на определении среднего темпа роста:
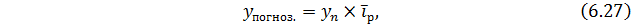
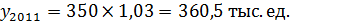
Рассмотренный прием экстраполяции предполагает, что уровни ряда изменятся в геометрической прогрессии.
3. Прогнозирование выполняется на основе аналитического выравнивания.
Для построения уравнения тренда используются различные математические функции.
Наиболее часто используются полиномы К-й степени.
Линейный тренд используется, если уровни динамического ряда изменяются с одинаковой скоростью, т.е. они изменяются в арифметической прогрессии. Тренд имеет вид:
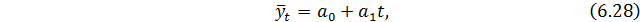
Используя данные того же примера, выполняется прогноз с использованием линейного тренда, для этого составляется расчетная таблица 6.8.
Таблица 6.8 Расчетная таблица
| Годы | 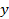
| t | 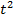
| Yt |
| -2 -1 | -620 -328 | |||
| Итого |
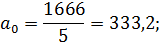
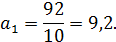
Уравнение прямой линии:
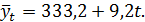
Подставляет вместо t значение 3 (условное обозначение последующего года) получаем:
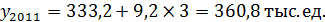
 2015-06-05
2015-06-05 451
451








